Paper Speedrun: Protostar
This article is cross-posted from the Geometry Notebook. Note that the ProtoStar paper has received many updates and some of the cross-term optimisations described in this speedrunm may no longer be up to date.
Title: ProtoStar: Generic Efficient Accumulation/Folding for Special Sound Protocols
Authors: Benedikt Bünz and Binyi Chen
Link: https://eprint.iacr.org/2023/620
TL;DR: ProtoStar presents three results: 1) a generic toolchain to obtain efficient folding schemes from special sound protocols, 2) a simple special sound protocol for Plonkup where the prover does not depend on the size of the lookup table and 3) a non-uniform IVC scheme based on the former results. Their folding scheme follows the same pattern described in Nova/Sangria (relaxation of the equations) but introduces an optimisation to avoid committing to cross-terms: instead of checking $l$ equations of degree $d$, ProtoStar batches them into a single equation of degree $(d+2)$ and $2\sqrt{l}$ equations of degree 2. The cross-terms from the degree-2 equations can be committed to using the Pedersen vector commitment (as in Nova) and those arising from the single high degree check can be committed to using the identity function (the “commitments” are still short enough and binding!).
ProtoStar is one of the latest instalments in a line of work concerned with constructing efficient IVC schemes (incrementally verifiable computation). It presents three important results:
- folding schemes for generic interactive protocols where the verifier is expressed as a series of equations (more formally, an algebraic check). These folding schemes are based on the techniques of Nova [KST22] / Sangria [Moh23] and introduce optimisations to avoid expensive commitments to cross-terms, especially when dealing with high degree gates.
- a 3-move interactive protocol for Plonkup relations (custom gates PLONK with lookups).
- a non-uniform IVC scheme (like SuperNova [KS22]) for Plonkup circuits.
We cover each of these results separately in the following sections.
Result 1: Folding for Special Sound Protocols
We start with the central result of the paper: how do we build a folding scheme for any “secure” interactive protocol?
Before we cover ProtoStar’s answer, we have a few notions to unpack:
- what do we mean by “folding scheme”?
- what notion of security are we using?
Folding / Accumulation Schemes
Recently, a lot of attention has been focused on constructing efficient schemes that realise incrementally verifiable computation (IVC). These parallel attempts have unfortunately led to the appearance of many formal definitions for variants of a generic class of protocols. Readers may already have come across the notions of nested amortisation [BGH19], aggregation [BDFG20], (atomic) accumulation [BCMS20], split accumulation [BCLMS21], folding [KST22] and/or multi-folding [KS23]. Here, we use the terms “folding scheme” to describe any scheme from this group of protocols.
The core idea of a folding scheme is to “fold” (combine, accumulate, compress, aggregate, etc…) instances of a problem that we are concerned with - the predicate - into a single problem - the accumulator. Often, the predicate will be the circuit satisfiability problem: given an arithmetic circuit and a partial wire assignments (the instance), the prover must demonstrate knowledge of a complete wire assignment (the witness) that would make the circuit evaluate to $0$ (or $1$ in some definitions). Choosing a corresponding accumulator is one of the differentiating features between folding schemes. In earlier schemes, the accumulator was the opening proof to a polynomial commitment. Later schemes such as Nova [KST22] use a “relaxed” variant of R1CS (a particular representation of the circuit satisfiability problem).
Folding schemes are formalised as interactive protocols between a Prover and a Verifier. The Prover is given an instance-witness pair from the predicate relation, $(x, w) \in \mathcal{R}$, and an instance-witness pair from the accumulator relation $(u, v) \in \mathcal{S}$. The verifier is only given the instances $x$ and $u$. At the end of the protocol, the prover outputs an updated accumulator $(u’, v’) \in \mathcal{S}$, and the verifier outputs the updated accumulator instance $u’$. The folding is performed such that:
- any party that knew the witnesses $w$ and $v$ can easily derive the witness $v’$. (Perfect completeness).
- any party that knows a valid witness for $u’$ must know (with overwhelming probability) valid witnesses for $x$ and $u$. (Knowledge soundness).
Importantly, it should be cheaper to fold instances and verify the resulting accumulator than simply verifying all the original instances.
Special Soundness
Now for the second key word in the paper’s title: “special sound protocols”. Special soundness is a property of interactive protocols. It states that given a tree of accepting transcripts (we will see what that is in a second), there exists an algorithm that can recover a valid witness.
A tree of transcripts is a tree in which each node is a prover message and each edge is verifier challenge. It allows to track what the prover would have sent given different challenges from the verifier. In that sense, the tree is like a multiverse of provers: at each step of the protocol, we branch into different universes where each universe has a different verifier challenge. Looking at the complete tree, each path from the root to one leaf represents the prover-verifier interaction in one of these related universes. Given this multiverse view, one should be able to “extract” the witness that the prover knows.
Note that in the real world we do not have this multiverse view, so special soundness does not introduce a vulnerability in your protocol.
[AFK22] present an important result for special sound protocols: applying the Fiat-Shamir transform to a special sound protocol produces a non-interactive argument of knowledge (NARK) that satisfies the knowledge soundness property. In other words, when we replace the verifier challenges by random oracle calls (Fiat-Shamir), there exists a generic method to obtain this tree of transcript in acceptable time; therefore the resulting NARK is secure.
Note that this method requires to “rewind” (read “debug”) the prover and therefore cannot be applied to a proof once it has been produced. Once again, no real-world attacks - phew.
The Folding Recipe
We are finally ready to describe ProtoStar’s generic folding scheme. ProtoStar considers special sound protocols with algebraic verifiers. These are protocols where the verifier checks that all of $l$ equations evaluate to $0$. The inputs to these equations are the public inputs, the prover’s messages and the verifier’s random challenge.
The recipe (or toolchain) goes as follows:
- Define a suitable accumulator (see “Commit-and-Open” and “Cross-term Compression” below).
- Compile the special sound protocol to a NARK using the Fiat-Shamir transform.
- Apply Nova/Sangria-style relaxation and random linear combinations to define a folding scheme.
Below, we show a partial diagram of this toolchain: Partial toolchain for the ProtoStar Folding Scheme.
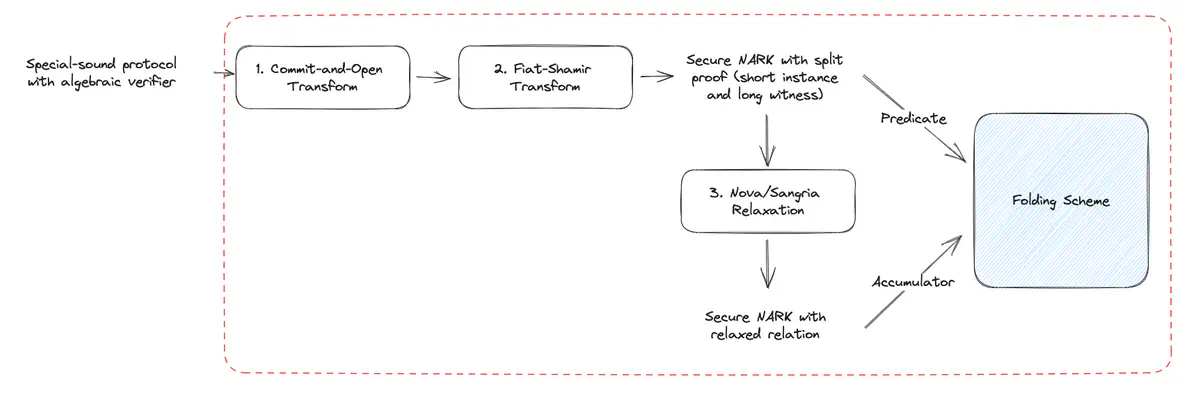
Commit-and-Open. To define an efficient accumulator, ProtoStar uses an additively homomorphic commitment scheme. Indeed, as explained in [BCLMS21], accumulators are particularly efficient when they can be broken into a short instance part and a longer witness part. Therefore, ProtoStar applies what they call the “Commit-and-Open” transform: rather than sending messages, the prover sends commitments to the messages prescribed by the protocol. In the last step, the prover sends all the messages in clear. Although this transformation introduces redundancy, it allows to create an accumulator where the instance is the collection of all commitments (short) and the witness is the collection of all messages (longer).
Accumulation. To define a folding scheme, ProtoStar applies the same relaxation technique described in Nova [KST22] and generalised by Sangria [Moh23]. Starting from the verifier equations, we introduce a new variable $u$ and use it to make each constraint into a homogenous function. Then, rather than checking that the $i$-th function evaluates to $0$, the verifier checks that it evaluates to some expected error $e_i$. For example:
$$ \begin{equation*} \begin{array}{c c c} \text{Original equation} & & \text{Relaxed equation} \\ f(X) = 5X + 3 X^2 = 0 &\rightarrow &f’(X, {\color{blue}{u}}) = 5{\color{blue}{u}}X + 3 X^2 = {\color{blue}{e_f}} \\ g(X, Y) = X^3 + 5X + 9 - Y^2 = 0 &\rightarrow &g’(X, Y, {\color{blue}{u}}) = X^3 + 5{\color{blue}{u^2}}X + 9{\color{blue}{u^3}} - {\color{blue}{u}}Y^2 = {\color{blue}{e_g}} \end{array} \end{equation*} $$
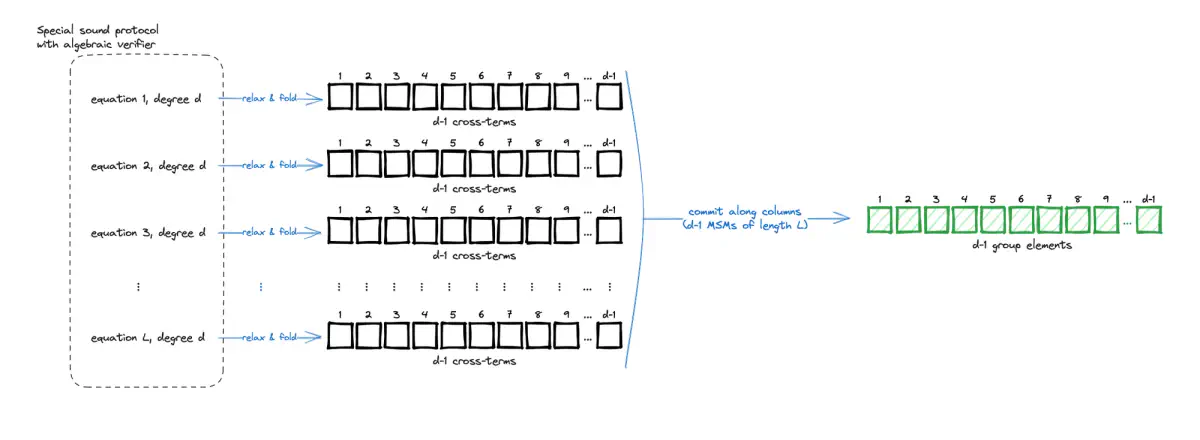
Unfortunately, the construction described so far runs into the same efficiency issue we came across in Sangria: a degree $d$ equation will produce $(d-1)$ cross-terms. Consider the functions $h_2(X) = X^2$ as a simple example of a degree-2 homogeneous function. Evaluating $h_2$ at some value $a+b$ yields 1 cross-term: $$ \begin{equation*} h_2(a+b) = a^2 + 2ab + b^2 = h_2(a) + {\color{red}{2ab}} + h_2(b) \end{equation*} $$ Similarly, for a degree-3 function $h_3(X) = X^3$, we would get 2 cross-terms: $$ \begin{equation*} h_3(a+b) = a^3 + 3a^2b + 3b^2a + b^3 = h_3(a) + {\color{red}{3a^2b + 3b^2a}} + h_3(b) \end{equation*} $$
As shown in the diagram below, accounting for $l$ equations of degree $d$, the relaxation method would produce $(d-1)$ cross-term vectors each of length $l$. Committing to these vectors would require the prover to perform $(d-1)$ MSMs (multi-scalar multiplications) of length $l$. This would constitute a clear performance bottleneck for the folding scheme.
Cross-term Compression
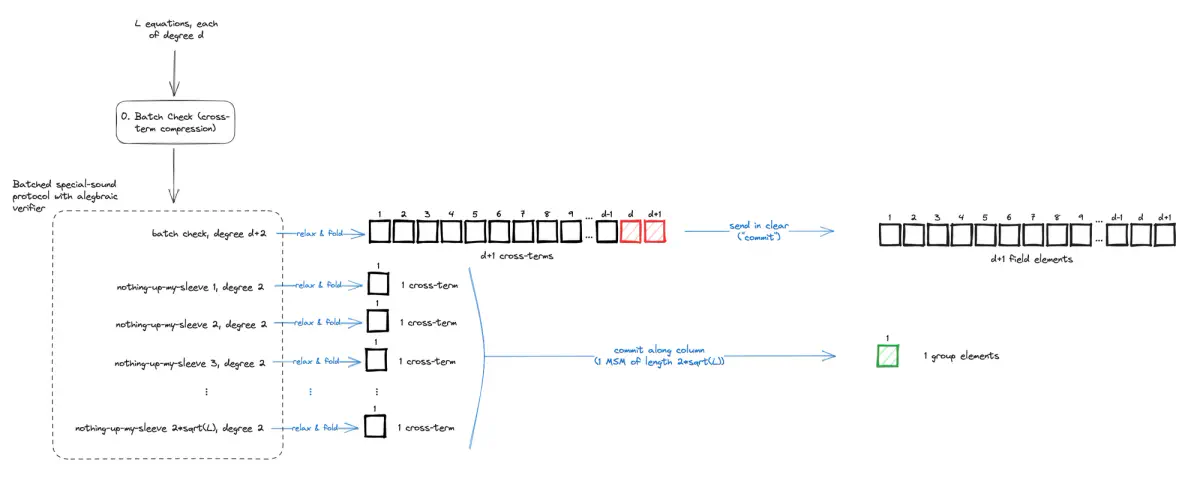
ProtoStar remediates this by introducing a 0th stage in the toolchain (see section 3.5 of the paper). Using an additional round of interaction, they modify the original protocol such that instead of checking that $l$ equations all evaluate to $0$, they run a single batch check on these equations and a series of low degree “nothing-up-my-sleeve” checks to convince the verifier that the batching was performed correctly. The end-to-end folding toolchain is shown below:
Full ProtoStar toolchain for generic folding, including cross-term optimizations.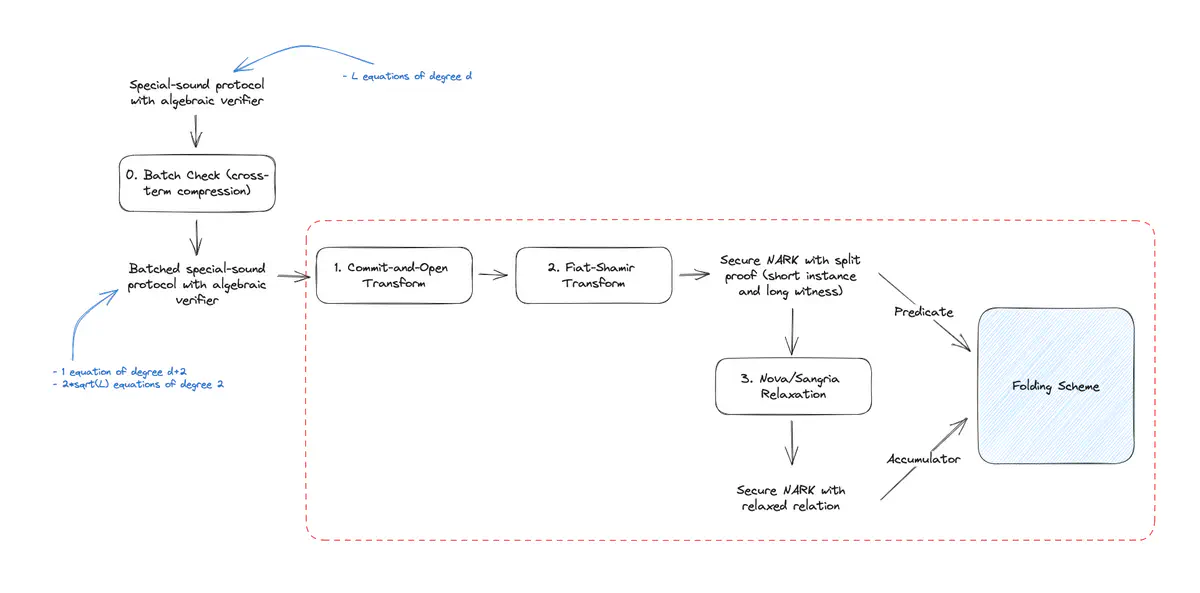
Random Linear Combination. The classic way to batch $l$ zero checks into one is to take a random linear combination of the values being checked. Omitting the arguments, let’s denote $v_1(\cdot), \dots, v_l(\cdot)$ the $l$ original verifier equations and $\beta_1, \dots, \beta_{l-1}$ the random batching coefficients. The batch check $v_{batch}(\cdot, \beta_1, \dots, \beta_{l-1})$ can be expressed as: $$ v_{batch}(\cdot, \beta_1, \dots, \beta_l) = v_1(\cdot) + \beta_1, v_2(\cdot) + \beta_2 , v_3(\cdot) + \dots + \beta_{l-1} , v_l(\cdot) $$
Notice that if all of the $v_i$ were of degree $d$, then $v_{batch}(\cdot, \beta_1, \dots, \beta_l)$ is of degree $d+1$.
Attempt 1. Rather than requiring $(l-1)$ random challenges from the verifier, the prover can take powers of a single random challenge $\mathsf{chal}$, i.e. $\beta_i = \mathsf{chal}^i$. From one challenge, the prover has artificially produced more challenges (!). These artificial challenges need to be checked by the verifier to ensure that the prover did not choose them in an advantageous manner. Therefore, the verifier also needs to check that $\beta_1 = \mathsf{chal}$ and $\beta_{i+1} = \beta_i * \beta_1$ (degree 1 and 2 respectively). These are the “nothing-up-my-sleeve” checks mentioned earlier!
Attempt 2. The method described above would require the prover to send a message containing all $(l-1)$ artificial challenges. A better trade-off can be obtained by getting the prover to produce two chains of challenges $\beta_1, \dots, \beta_{\sqrt{l} - 1}$ and $\gamma_1, \dots, \gamma_{\sqrt{l} - 1}$ as shown below: $$ \begin{align*} &\beta_1 = \mathsf{chal}, ; \beta_2 = \mathsf{chal}^2, ; \dots, ; \beta_{\sqrt{l} - 1} = \mathsf{chal}^{\sqrt{l} - 1} \\ &\gamma_1 = \mathsf{chal}^{\sqrt{l}}, ; \gamma_2 = \mathsf{chal}^{2\sqrt{l}}, ; \dots, ; \gamma_{\sqrt{l} - 1} = \mathsf{chal}^{(\sqrt{l} - 1)\sqrt{l}} \\ \end{align*} $$ Concretely, for $l=16$, the $\beta$ values would be $(\beta_1 = \mathsf{chal}, \beta_2 = \mathsf{chal}^2, \beta_3 = \mathsf{chal}^3)$ and the $\gamma$ value would be $(\gamma_1 = \mathsf{chal}^4, \gamma_2 = \mathsf{chal}^8, \gamma_3 = \mathsf{chal}^{12})$. Importantly, any power of $\mathsf{chal}$ can be computed from a single multiplication between a $\beta_i$ and a $\gamma_j$ value, e.g. $\mathsf{chal}^{10} = \beta_2 \cdot \gamma_2$. Therefore, the verifier can still perform the nothing-up-my-sleeve checks using only degree-1 and degree-2 equations. The multiplication between $\beta_i$ and $\gamma_j$ values will also arise in the batch check equation to construct the batching coefficient, therefore raising its degree to $(d+2)$.
At this point, the reader may be wondering whether this whole process has been counter-productive. Indeed, the verifier now has to relax and accumulate an equation of degree $d+2$. ProtoStar’s idea is that there is only one equation of such degree and the total number of cross-terms has been reduced: $d+1$ cross-terms for the batch check, and $1$ cross-term for each of the $2\sqrt l$ nothing-up-my-sleeve checks.
Furthermore, the cost of committing to the cross-terms can also be reduced. Rather than using a Pedersen commitment for all the cross-terms, ProtoStar uses Pedersen for the cross-terms that arise from equations of degree 2 (like Nova) but use the identity function as a trivial commitment for the equation of high degree. The resulting costs and proof size are summarised in the diagram and table below.
| Before compression | After compression | |
|---|---|---|
| Number of equations | $l$ | $1$ (the batch check) $+$ $2\sqrt{l}$ (the nothing-up-my-sleeve checks) |
| Degrees of equations | $d$ | $d +2$ (one equation), $2$ or less ($2\sqrt{l}$ equations) |
| Number of cross-terms (in $\mathbb{F}$ elements) | $l*(d-1)$ | $d+1 + 2\sqrt{l}$ |
| Cross-term commitment cost | $(d-1)$ MSMs of length $l$ | $1$ MSM of length $2\sqrt{l}$ |
| Cross-term commitment size | $(d-1)$ $\mathbb{G}$ elements | $(d+1)$ $\mathbb{F}$ elements and $1$ $\mathbb{G}$ element |
Result 2: Special-Sound Protocol for Plonkup Relations
Having established the above toolchain for efficient folding schemes, the authors proceed to describe special-sound protocols with algebraic verifiers for Plonkup relations (high degree custom gates, copy constraints and lookup tables). The authors are not concerned with achieving succinctness or zero-knowledge: this can be achieved at a later stage, as done in Nova [KST22].
Gate and Copy Constraints
The protocols for proving the gate equation and the copy constraints are trivial: the prover sends a claimed witness and the verifier checks the corresponding equation(s).
Lookup Arguments
To prove lookup relations, ProtoStar uses the “set inclusion” lemma from [Hab22] (Lemma 5): the elements of a witness vector $\mathbf{w} \in \mathbf{F}^l$ all appear in the “table” $\mathbf{t} \in \mathbf{F}^T$ if and only if there exists a vector $\mathbf{m} \in \mathbf{F}^T$ of multiplicities such that $$ \sum_{i=1}^l \frac{1}{\mathbf{w}i + X} = \sum{i=1}^T \mathbf{m}_i \cdot \frac{1}{\mathbf{t}_i + X} $$
The vector $\mathbf{m}$ provides a count of how many times each element of $\mathbf{t}$ is present in $\mathbf{w}$, as made explicit by the concrete example below:
| Witness $\mathbf{w}$ | Table $\mathbf{t}$ | Multiplicities $\mathbf{m}$ | |
|---|---|---|---|
| 2 | 1 | 0 | |
| 2 | 2 | 2 | |
| 6 | 3 | 0 | |
| 4 | 0 | ||
| 5 | 0 | ||
| 6 | 1 | ||
| 7 | 0 | ||
| 8 | 0 | ||
| 9 | 0 |
To get intuition as to why the lemma holds, consider the LHS and RHS of the equation: the LHS creates a “target” sum of ratios of the form $\frac{1}{\mathbf{w}_i + X}$; the RHS has access to all the possible ratios built from the table (these are the $\frac{1}{\mathbf{t}_i + X}$) and must use the vector $\mathbf{m}$ to pick which ratios are required to reach the target.
The lemma’s equation can be checked by evaluating both sums at the same randomly chosen point (Schwartz-Zippel lemma) as done by the following protocol:
- the prover sends all terms that are required to construct the ratios, effectively sending $\mathbf{w}$ and $\mathbf{m}$. ($\mathbf{t}$ is public).
- the verifier sends a random challenge $r$.
- the prover computes and sends all the $\frac{1}{\mathbf{w}_i + r}$ and $\frac{\mathbf{m}_i}{\mathbf{t}_i + r}$ ratios. The verifier checks the well-formation of these ratios and the equality of the sums.
Efficiency. The protocol is highly efficient:
- the prover’s work and messages do not depend on the size of the table. This is because as highlighted by our example, the vector $\mathbf{m}$ is sparse (most of its elements are $0$). Similarly, most of the $\frac{\mathbf{m}_i}{\mathbf{t}_i + r}$ ratios will be $0$. On the other hand, the accumulated $\mathbf{m}$ vector will not be sparse. However this specific vector can be cached, with updates only affecting a low number of entries (as the incoming $\mathbf{m}$ is sparse).
- the verifier only checks degree-$2$ equations (or $3$ if we need perfect completeness).
- the accumulation work is also independent of the table assuming that $\mathbf{m}$ is sparse.
Lookups (vector-valued). In practice, we are interested in performing lookups for vector values rather than single field elements as in the protocol above. Vector-valued lookups allow to perform efficient range checks or efficient bit operations.
The standard technique is to collapse the columns of the vector-value into a single value by performing a weighted sum across columns with verifier challenges. ProtoStar is no exception. As in the “cross-term compression” section, rather than using $c-1$ verifier challenges, the prover can compute powers of a single challenge. This requires sending an additional message containing all $c-1$ powers of the challenge, and raises the degree of the verifier checks from $2$ as above, to $3$.
Plonkup
Bringing this all together in a single protocol for Plonkup relations is simple: the prover only sends one witness and the verifier performs the checks (and subsequent interactive rounds) from all three protocols described above on this single witness.
Combining results 1 and 2, one can now build an IVC scheme comparable to Nova without the final “compression” SNARK. This scheme however supports circuits with high degree gates (at a low accumulation cost) and lookup tables.
Result 3: Non-uniform IVC for Plonkup Circuits
Non-uniform IVC (NIVC) is introduced in SuperNova [KS22] and described incrementally verifiable computations where each step of the computation executes one of many circuits. This is in contrast to classical (or uniform) IVC, where the same circuit is applied at every step.
ProtoStar devise a NIVC scheme by describing a special sound protocol for non-uniform Plonkup relations. This protocol allows the verifier to check different sets of equations depending on the current state of the program counter (a variable included in the public inputs). This program counter acts as a selector for which verifier equations need to be used.
Acknowledgements
Thank you to Kobi Gurkan, Ying Tong Lai and Tom Walton-Pocock for their thorough review and helpful comments.
References
[AFK22] Attema, Thomas, Serge Fehr, and Michael Klooß. “Fiat-shamir transformation of multi-round interactive proofs.” Theory of Cryptography: 20th International Conference, TCC 2022, Chicago, IL, USA, November 7–10, 2022, Proceedings, Part I. Cham: Springer Nature Switzerland, 2022.
[BC23] Bünz, Benedikt, and Binyi Chen. “ProtoStar: Generic Efficient Accumulation/Folding for Special Sound Protocols.” Cryptology ePrint Archive (2023).
[BCLMS21] Bünz, Benedikt, Alessandro Chiesa, William Lin, Pratyush Mishra, and Nicholas Spooner. “Proof-carrying data without succinct arguments.” In Advances in Cryptology–CRYPTO 2021: 41st Annual International Cryptology Conference, CRYPTO 2021, Virtual Event, August 16–20, 2021, Proceedings, Part I 41, pp. 681-710. Springer International Publishing, 2021.
[BCMS20] Bünz, B., Chiesa, A., Mishra, P., & Spooner, N. (2020). Proof-carrying data from accumulation schemes. Cryptology ePrint Archive.
[BDFG20] Boneh, D., Drake, J., Fisch, B., & Gabizon, A. (2020). Halo infinite: Recursive zk-snarks from any additive polynomial commitment scheme. Cryptology ePrint Archive.
[BGH19] Bowe, S., Grigg, J., & Hopwood, D. (2019). Recursive proof composition without a trusted setup. Cryptology ePrint Archive.
[Hab22] Haböck, Ulrich. “Multivariate lookups based on logarithmic derivatives.” Cryptology ePrint Archive (2022).
[KS22] Kothapalli, Abhiram, and Srinath Setty. “SuperNova: Proving universal machine executions without universal circuits.” Cryptology ePrint Archive (2022).
[KS23] Kothapalli, Abhiram, and Srinath Setty. “HyperNova: Recursive arguments for customizable constraint systems.” Cryptology ePrint Archive (2023).
[KST22] Kothapalli, Abhiram, Srinath Setty, and Ioanna Tzialla. “Nova: Recursive zero-knowledge arguments from folding schemes.” Advances in Cryptology–CRYPTO 2022: 42nd Annual International Cryptology Conference, CRYPTO 2022, Santa Barbara, CA, USA, August 15–18, 2022, Proceedings, Part IV. Cham: Springer Nature Switzerland, 2022.
[Moh23] Mohnblatt, Nicolas. “Sangria: a Folding Scheme for PLONK”. Online https://github.com/geometryresearch/technical_notes/blob/main/sangria_folding_plonk.pdf (2023)