Nicolas Mohnblatt

Sangria: a Folding Scheme for PLONK

This article is cross-posted from the Geometry Notebook.

Edit 21/02. Remove the need for a commitment to $\mathbf{q_C}$ in the verifier key; improved strategy for higher degree custom gates thanks to feedback from Nat Bunner and Lev Soukhanov.

As shown in Nova [KST22], incrementally verifiable computation (IVC) can be realised using a folding scheme and a zkSNARK. In this article, we present a folding scheme for a variant of the PLONK arithmetization [GWC19]. We then extend our relaxed PLONK arithmetization to accept custom gates of degree 2 and circuits with higher gate arity. Finally we outline avenues for future work including folding higher degree gates, supporting lookup gates and designing an IOP for the relaxed PLONK arithmetization.

⚠️ This article is a condensed version of the Sangria technical note. See the full version for proofs and extended discussions. We assume the reader is familiar with IVC and Nova. Suggested preliminary viewing and reading: Justin Drake’s ZK Whiteboard Session and this Lambdaclass blog entry.

Preliminaries

PLONK Arithmetization

In PLONK, computations are represented as a matrix $\mathbf{M}$ with three columns $\mathbf{a}, \mathbf{b}, \mathbf{c}$ and $n+s+1$ rows. $n$ is the number of public inputs, $s$ is the number of gates and the extra row checks that the final result is 1 (i.e. that the circuit is satisfied).

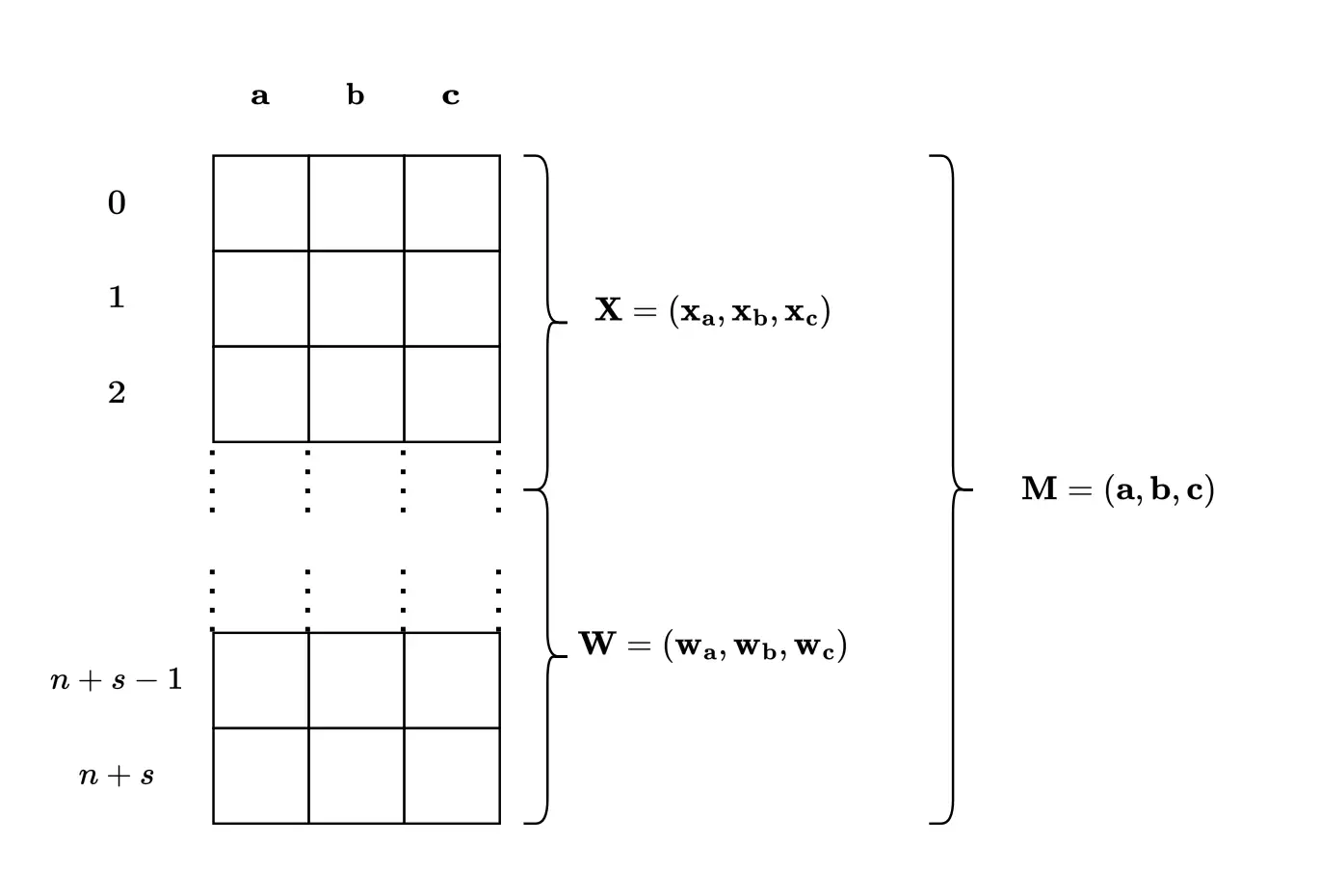
A PLONK computation trace.

A PLONK computation trace.

The values at the $i$-th row – $\mathbf{a} _ i, \mathbf{b} _ i, \mathbf{c} _ i$ – correspond respectively to the left input, right input and output of the $i$-th gate. The $i$-th gate is defined as: $$ C_{\mathcal{Q}, i}(\mathbf{a}, \mathbf{b}, \mathbf{c}) := (\mathbf{q_L})_i\mathbf{a} _ i + (\mathbf{q_R})_i\mathbf{b} _ i + (\mathbf{q_O})_i\mathbf{c} _ i + (\mathbf{q_M})_i\mathbf{a} _ i\mathbf{b} _ i + (\mathbf{q_C})_i $$

where $(\mathbf{q_L})_i, (\mathbf{q_R})_i, (\mathbf{q_O})_i, (\mathbf{q_M})_i, (\mathbf{q_C})_i$ are the $i$-th value of each selector vector. We denote $\mathcal{Q} = \left\{\mathbf{q_L}, \mathbf{q_R}, \mathbf{q_O}, \mathbf{q_M}, \mathbf{q_C} \right\}$ the set of selector vectors.

Gates are “wired” together using copy constraints enforcing for example that $\mathbf{a} _ 3 = \mathbf{c} _ 1$ – the left input to Gate 3 is the output of Gate 1. We denote $\mathcal{S}$ the set of copy constraints.

A circuit is fully defined by the tuple $(\mathcal{Q}, \mathcal{S})$.

Folding Schemes

The Nova paper introduces folding schemes and provide the following intuitive definition:

[…] a folding scheme for a relation $\mathcal{R}$ is a protocol that reduces the task of checking two instances in $\mathcal{R}$ to the task of checking a single instance in $\mathcal{R}$.

The full definition is given in the paper under Definition 6.

Commitment Schemes

Our scheme makes use of a hiding and binding additively homomorphic commitment scheme for vectors of elements in a finite field $\mathbb{F}$. We denote such a scheme as $\mathsf{Com}$ and write $\overline{A} = \mathsf{Com}(\mathsf{pp} _ C, \mathbf{a};{r})$ a commitment to the vector $\mathbf{a}$ using randomness value $r \in \mathbb{F}$ and commitment parameters $\mathsf{pp} _ C$.

Sangria

Nova builds a folding scheme for the R1CS arithmetization. Here we present a folding scheme for the PLONK arithmetization. We use the same insights as Nova:

Relaxed PLONK Gate Equation

For a scalar $u \in \mathbb{F}$ and error (or slack) vector $\mathbf{e} \in \mathbb{F}^{n+s+1}$ we define the relaxed PLONK gate equation as: $$ \begin{equation} C’_{\mathcal{Q}, i}(\mathbf{a}, \mathbf{b}, \mathbf{c}, u, {\mathbf{e}}) := {u}\left[(\mathbf{q_L})_i\mathbf{a} _ i + (\mathbf{q_R})_i\mathbf{b} _ i + (\mathbf{q_O})_i\mathbf{c} _ i \right] + (\mathbf{q_M})_i\mathbf{a} _ i\mathbf{b} _ i + u^2 (\mathbf{q_C})_i + {\mathbf{e} _ i} \end{equation} $$ Copy constraints in relaxed PLONK are identical to the PLONK copy constraints. A relaxed PLONK trace is represented by the tuple $(\mathbf{a}, \mathbf{b}, \mathbf{c}, u, \mathbf{e})$.

For a PLONK instance-witness pair $(\mathbf{X}, \mathbf{W})$, we define a relaxed PLONK instance-witness pair $(U, W)$ as: $$ \begin{align} U &:= (\mathbf{X}, u, \overline{W_a}, \overline{W_b}, \overline{W_c}, \overline{E}) \\ W &:= (\mathbf{W}, \mathbf{e}, r_a, r_b, r_c, r_{e}) \end{align} $$ where $\overline{W_a} = \mathsf{Com}({\mathsf{pp} _ W},{\mathbf{w_a}};{r_a})$, $\overline{W_b} = \mathsf{Com}({\mathsf{pp} _ W},{\mathbf{w_b}};{r_b})$, $\overline{W_c} = \mathsf{Com}({\mathsf{pp} _ W},{\mathbf{w_c}};{r_c})$ and $\overline{E} = \mathsf{Com}({\mathsf{pp} _ E},{\mathbf{e}};{r_e})$.

Importantly, any PLONK relation can be transformed into a relaxed PLONK relation by setting $u=1$, $\mathbf{e} = \overrightarrow{0}$ and providing the necessary commitments. Thus the relaxed PLONK arithmetization is $\mathsf{NP}$-complete.

Folding Scheme for Relaxed PLONK

Following the notation from Nova, a folding scheme is defined by 4 algorithms $\mathcal{G}, \mathcal{K}, \mathcal{P}, \mathcal{V}$:

The verifier $\mathcal{V}$ is given the verifier key $\mathsf{vk}$ and two committed relaxed PLONK instances, $\left(\mathbf{X’}, u’, \overline{W’_a}, \overline{W’_b}, \overline{W’_c}, \overline{E’} \right)$ and $\left(\mathbf{X’’}, u’’, \overline{W’’_a}, \overline{W’’_b}, \overline{W’’_c}, \overline{E’’} \right)$. The prover $\mathcal{P}$ is given the prover key $\mathsf{pk}$ and both instances with their corresponding witnesses $\left( \mathbf{W’}, \mathbf{e’}, r’_a, r’_b, r’_c, r’ _ {e} \right)$ and $\left( \mathbf{W’’}, \mathbf{e’’}, r’’_a, r’’_b, r’’_c, r’’ _ {e} \right)$.

The Sangria folding scheme proceeds as follows:

  1. $\mathcal{P}$ samples $r_t$ at random and sends $\overline T = \mathsf{Com}({\mathsf{pp} _ E},{\mathbf{t}};{r_t})$ where $\mathbf{t}$ is computed as: $$\begin{align} \mathbf{t} &:= u’’(\mathbf{q_L}\circ\mathbf{a’} + \mathbf{q_R}\circ\mathbf{b’} + \mathbf{q_O}\circ\mathbf{c’}) + u’(\mathbf{q_L}\circ\mathbf{a’’} + \mathbf{q_R}\circ\mathbf{b’’} + \mathbf{q_O}\circ\mathbf{c’’}) \\ &\qquad + \mathbf{q_M} \circ (\mathbf{a’}\circ\mathbf{b’’} + \mathbf{a’’}\circ\mathbf{b’}) \\ &\qquad + 2ru’u’’ \mathbf{q_C} \end{align}$$ where $\circ$ denotes element-wise multiplication.
  2. $\mathcal{V}$ samples the challenge $r$ at random.
  3. $\mathcal{P}$ and $\mathcal{V}$ output the folded instance $(\mathbf{X}, u, \overline{W_a}, \overline{W_b}, \overline{W_c}, \overline{E})$ where: $$ \begin{align} \mathbf{X} &\leftarrow \mathbf{X’} + r\mathbf{X’’} \\ u &\leftarrow u’ + ru’’ \\ \overline{W_a} &\leftarrow \overline{W’_a} + r\overline{W’’_a} \\ \overline{W_b} &\leftarrow \overline{W’_b} + r\overline{W’’_b} \\ \overline{W_c} &\leftarrow \overline{W’_c} + r\overline{W’’_c} \\ \overline{E} &\leftarrow \overline{E’} - r\overline{T} + r^2 \overline{E’’} \end{align} $$
  4. $\mathcal{P}$ outputs the folded witness $\left( \mathbf{W}, \mathbf{e}, r_a, r_b, r_c, r_e \right)$ where: $$ \begin{align} \mathbf{W} &\leftarrow \mathbf{W’} + r\mathbf{W’’} \\ r_a &\leftarrow r’_ {a} + r \cdot r’’_ {a} \\ r_b &\leftarrow r’_ {b} + r \cdot r’’_ {b} \\ r_c &\leftarrow r’_ {c} + r \cdot r’’_ {c} \\ \mathbf{e} &\leftarrow \mathbf{e’} - r\mathbf{t} + r^2 \mathbf{e’’} \\ r_e &\leftarrow r’_ {e} - r \cdot r_t + r^2 \cdot r’’_ {e}
    \end{align} $$

Theorem: The above construction is a public-coin folding scheme for the committed relaxed PLONK arithmetization with perfect completeness, knowledge soundness, and zero-knowledge.

Proof intuition. Perfect completeness can be shown by following the algebra until establishing that $$ C’_ {\mathcal{Q}, i}(\mathbf{a}, \mathbf{b}, \mathbf{c}, u, \mathbf{e}) = C’_ {\mathcal{Q}, i}(\mathbf{a’}, \mathbf{b’}, \mathbf{c’}, u’, \mathbf{e’}) + r^2 C’_ {\mathcal{Q}, i}(\mathbf{a’’}, \mathbf{b’’}, \mathbf{c’’}, u’’, \mathbf{e’’}) $$ We also show that copy constraints are preserved.

We prove knowledge soundness using the same strategy as [KST22]. Specifically, we apply the forking lemma for folding schemes (Lemma 1 in [KST22]) to obtain three transcripts. We then show that the extractor uses all three transcripts to interpolate the original $\mathbf{e’}, r’_e$ and $\mathbf{e’’}, r’’_e$ values, and any two transcripts to interpolate the values $(\mathbf{W’}, r’_a, r’_b, r’_c)$ and $(\mathbf{W’’}, r’’_a, r’’_b, r’’_c)$. We then show that the interpolated values belong to traces that each satisfy the circuit’s gate equalities and copy constraints.

Finally zero-knowledge holds as the prover’s messages are hiding commitments and the verifier only sends a public random value. A proof is presented in the full technical note. $\square$

Degree 2 Custom Gates

We write a degree 2 custom gate and its selector as: $$ \begin{equation} G_i(\mathbf{a}, \mathbf{b}, \mathbf{c}) := (\mathbf{q_G})_i \cdot g(\mathbf{a} _ i, \mathbf{b} _ i, \mathbf{c} _ i) \end{equation} $$

To fold such a gate, write $g$ as a sum of monomials and separate the monomials by their degrees. Let $g_C$, $g_1$ and $g_2$ be the sums of the constant, degree 1 and degree 2 monomials respectively. We can write the relaxed constraint equation as:

$$ \begin{align} C’_{\mathcal{Q}, i}(\mathbf{a}, \mathbf{b}, \mathbf{c}, u, \mathbf{e}) &:= u\left[(\mathbf{q_L})_i\mathbf{a} _ i + (\mathbf{q_R})_i\mathbf{b} _ i + (\mathbf{q_O})_i\mathbf{c} _ i + {(\mathbf{q_G})_i \cdot g_1(\mathbf{a} _ i, \mathbf{b} _ i, \mathbf{c} _ i)} \right] \\ &\qquad + (\mathbf{q_M})_i\mathbf{a} _ i\mathbf{b} _ i + {(\mathbf{q_G})_i \cdot g_2(\mathbf{a} _ i, \mathbf{b} _ i, \mathbf{c} _ i)} + u^2 (\mathbf{q_C})_i + u^2 {(\mathbf{q_G})_i \cdot g_C} + \mathbf{e} _ i \end{align} $$

Folding $(\mathbf{a’}, \mathbf{b’}, \mathbf{c’}, u’, \mathbf{e’})$ with $(\mathbf{a’’}, \mathbf{b’’}, \mathbf{c’’}, u’’, \mathbf{e’’})$ is still performed by taking random linear combinations, however the $\mathbf{t}$ vector must be adjusted to absorb the cross terms that arise from each of the following degree 2 expressions:

Higher Fan-In and Fan-Out

The current scheme can support higher arity circuits as long as the degree of the gate equation is smaller or equal to 2. Each additional gate input or output requires an additional witness column commitment.

Future Work

This note establishes a folding scheme for the standard PLONK arithmetization and introduces some customisation features. We conclude by briefly highlighting directions for future (and upcoming) work.

Succinct IVC using a zkSNARK for Sangria

Nova shows that a folding scheme directly implies IVC. However those IVC proofs are neither succinct nor zero-knowledge. To achieve both of these properties, one must devise a zkSNARK for the newly relaxed arithmetization. One possible direction is to convert the Sangria trace into a PLONKish trace with an extra witness column for the slack vector. Another direction would be to modify the IOP directly to manage the newly introduced $u$ and $\mathbf{e}$ values.

Lower Recursion Overhead

In the current construction, the folding verifier works with 1 commitment per witness column. The scheme can also work by flattening the witness matrix $\mathbf{W}$ into a single column vector, thus allowing the verifier to work with a single witness commitment (as in Nova). Doing so requires the reference string $\mathsf{pp} _ W$ to be three times longer for a circuit with “fan-in 2, fan-out 1” gates. It might also introduce extra checks and commitment openings later in the full IVC scheme given that the standard PLONK IOP uses commitments to each witness column.

Higher Degree Custom Gates

Higher degree custom gates can be achieved in the “random linear combination” folding strategy. Let $d$ be the highest degree of our constraint equation, the overall strategy is the following:

  1. Express the non-relaxed constraint equation $C_{\mathcal{Q}, i}$ as a sum of monomials.
  2. Use powers of the relaxation factor $u$ to make $C_{\mathcal{Q}, i}$ into a homogeneous degree $d$ polynomial.
  3. Add an error term $\mathbf{e}$ to absorb cross-terms. Cross terms will now have powers of $r$ from $1$ to $d-1$. We collect them respectively into the vectors $\mathbf{t_1}, \mathbf{t_2, \dots, \mathbf{t_{d-1}}}$ such that $$ \begin{equation} \mathbf{e} = \mathbf{e’} - \sum_{k=1}^{d-1} r^{k}\mathbf{t_k} + r^d\mathbf{e’’} \end{equation} $$
  4. Fold as described in the standard construction with the following modifications:
    • Prover computes and sends commitments to each of the $\mathbf{t_k}$ vectors.
    • Compute $\mathbf{e}$ as defined in the equation above and apply the corresponding operation in the commitment space.

Costs. This strategy introduces extra work for both the verifier and the prover. To compute the $d-1$ cross-term vectors and their commitments, the prover will perform $\mathcal{O}(d*(n+s))$ field operations and $\mathcal{O}(d*(n+s))$ point additions. Similarly, working in the commitment space, the verifier computes $\mathcal{O}(d)$ point additions. Note that the verifier work remains constant with respect to the security parameter and the circuit size. It does however call for a closer comparison between the folding and split accumulation [BCLMS20] approaches to achieve IVC.

Degree 3. A suggestion using the random linear combination strategy for degree 3 gates using the above strategy: $$ \begin{equation} u^2 \left[(\mathbf{q_L})_i\mathbf{a} _ i + (\mathbf{q_R})_i\mathbf{b} _ i + (\mathbf{q_O})_i\mathbf{c} _ i \right] + u (\mathbf{q_M})_i\mathbf{a} _ i\mathbf{b} _ i + (\mathbf{q _ {3}})_i \mathbf{a} _ i \mathbf{b} _ i \mathbf{c} _i + u^3 (\mathbf{q_C})_i + \mathbf{e}_i \end{equation} $$

where the error term is appropriately adjusted to absorb cross terms (see full note for an explicit representation of the cross terms).

Lookup Gates

PLONKish arithmetizations differentiate themselves from R1CS in part by their ability to integrate lookup arguments. We are keen to preserve this flexibility by developing folding strategies for lookup-enabled arithmetizations.

Acknowledgments

Thank you to Nat Bunner and Lev Soukhanov for their improvements to the high degree gate folding strategy. We also thank Andrija Novakovic, Lai Ying Tong, Kobi Gurkan and Koh Wei Jie for their helpful inputs and contribution.

References

[BCLMS20] Benedikt Bunz, Alessandro Chiesa, William Lin, Pratyush Mishra, and Nicholas Spooner. Proof-carrying data without succinct arguments. Cryptology ePrint Archive, Paper 2020/1618, 2020. https://eprint.iacr.org/2020/1618

[GWC19] Gabizon, Ariel, Zachary J. Williamson, and Oana Ciobotaru. Plonk: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge. Cryptology ePrint Archive, Paper 2019/953, 2019. https://eprint.iacr.org/2019/953

[KST22] Kothapalli, Abhiram, Srinath Setty, and Ioanna Tzialla. “Nova: Recursive zero-knowledge arguments from folding schemes.” Annual International Cryptology Conference. Springer, Cham, 2022. https://eprint.iacr.org/2021/370

#Geometry Notebook #Folding