Proximity Gaps: What Happened and How Does It Affect our SNARKs

This article is cross-posted from the ZK Security blog.

If you’ve been following the ZK space recently, you are likely to have heard about a flurry of recent results that disprove the proximity gaps conjecture. This conjecture was used to set parameters for hash-based SNARKs. As a consequence, many commentators were quick to call it a huge blow for SNARKs. So the big question is: how bad is it really?

In this post, I want to give you some visual intuition for what happened and explain how the results affect currently deployed SNARKs. I will attempt to do so without taking a journey through the wonderful moon math that enables all our protocols. If you are interested in learning about the moon math, please let us know! A “Proximity Gaps 201” article is never off the cards.

At the time of writing, there are 6 papers related to Reed-Solomon codes and proximity gaps that were released within the span of a week:

1. Diamond and Gruen, On the Distribution of the Distances of Random Words, (ePrint).
2. Crites and Stewart, On Reed–Solomon Proximity Gaps Conjectures (ePrint).
3. Bordage, Chiesa, Guan and Manzur, All Polynomial Generators Preserve Distance with Mutual Correlated Agreement (ePrint).
4. Goyal and Guruswami, Optimal Proximity Gaps for Subspace-Design Codes and (Random) Reed-Solomon Codes (ePrint).
5. Ben-Sasson, Carmon, Haböck, Kopparty and Saraf, On Proximity Gaps for Reed–Solomon Codes (ePrint).
6. Chatterjee, Harsha and Kumar, Deterministic list decoding of Reed-Solomon codes (ECCC).

I will only focus on papers that disprove the conjecture. Those are papers 1, 2 and 5 above. For short, I will refer to them using the authors’ initials: DG, CS and BGHKS respectively.

The visuals and some of the explanations used in this article are based on a slide presented by Angus Gruen in ethproofs call #6. You can also play around with the parameters of the graph using this lovely interactive tool built by Mahdi Sedaghat (Soundness Labs).

Before we begin

To understand what happened, let us first explain what the state-of-the-art was before all the new papers.

At a very high level, SNARKs make use of error-correcting codes to introduce redundancy and allow the verifier to check properties without reading the entirety of the prover’s inputs. To make sure encoding was done correctly, SNARKs also use a proximity test.

The efficiency and security of the SNARK depends on the parameters of the code and the proximity test. While there are many parameters to play with, we will focus on:

• the rate $\rho$ of the code. This is a measure of how much redundancy the code introduces. To be precise, it is the inverse of the amount of redundancy: $\rho = 1/2$ means that the encoding of a message is 2x larger than the message, $\rho = 1/4$ means a 4x blowup, etc… Our SNARKs usually require the denominator to be a power of two and therefore we will focus of values of $\rho$ between $0$ and $1/2$.
• the proximity parameter $\delta$ of the proximity test. This is a value between $0$ and $1-\rho$ and is the threshold for what the test considers to be “far” from the code. For readers familiar with the notion of relative Hamming distance: the proximity test is tuned such that all inputs that have distance greater than $\delta$ are rejected with high probability.

Choosing values for these parameters requires to balance a couple of trade-offs. The rate $\rho$ sets a pure performance trade-off: prover time vs proof size and verifier time. On the other hand, the proximity parameter $\delta$ tunes a performance vs security trade-off. Larger values of $\delta$ give a better prover time, verifier time and proof size! This is highly desirable. However, the mathematical state-of-the-art is not good enough to set $\delta$ to be arbitrarily large.

The image below shows all possible choices of $\rho$ and $\delta$ and defines multiple regions:

• The black region represents invalid parameters. As we said above, $\delta$ must be smaller than $1-\rho$.
• The green and blue zones represent parameter sets for which we have mathematical proofs of their security. Parameters in both zones give us a guarantee that the input to the proximity test is either $\delta$-close to the code, or will be rejected with high probability. In addition, parameters in the green zone guarantee that the input to the test is close to a unique codeword.
• Parameters in the white zone have unknown behaviour. We have no proof that they yield a secure proximity test. Operating in this zone represents a trade-off: we gain performance from using larger values of $\delta$, however we lose the mathematical guarantees for the protocol’s security.

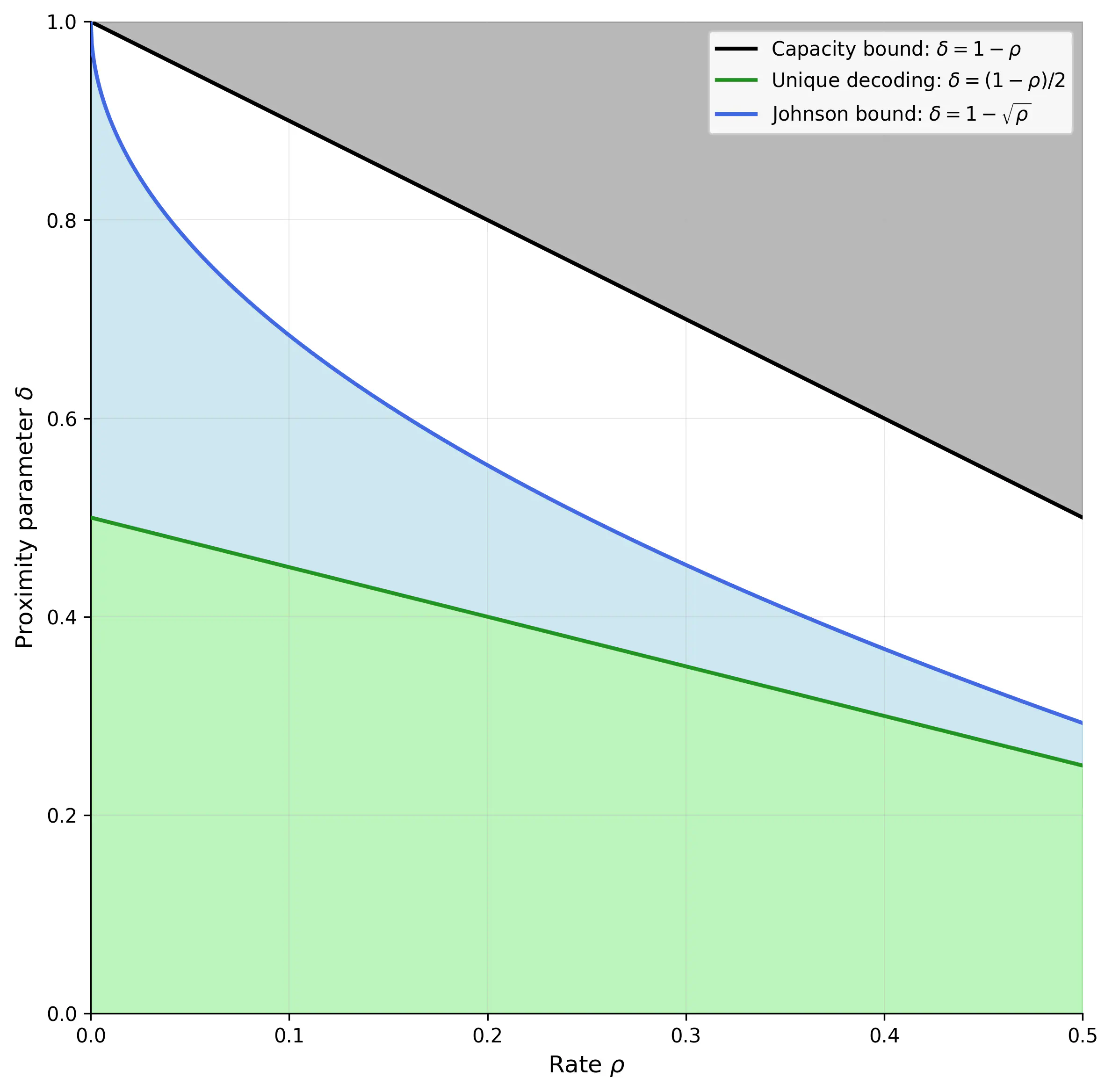
The open question therefore is: “what happens inside the white area?”. So far, many projects took the approach of assuming that the parameters in the white area are secure. This assumption is (roughly) what the proximity gaps conjecture states.

New results

The new results partially solve this question and relates it to other mathematical problems. We’ll cover both of these aspects separately.

Understanding the white area

The first result, which appears in different forms in DG, CS and BCHKS, is that some of the parameter choices in the white area are not safe to use. You can see this in the image below where I have plotted the same graph as before but also drew an approximation of the new red area as formulated in DG.

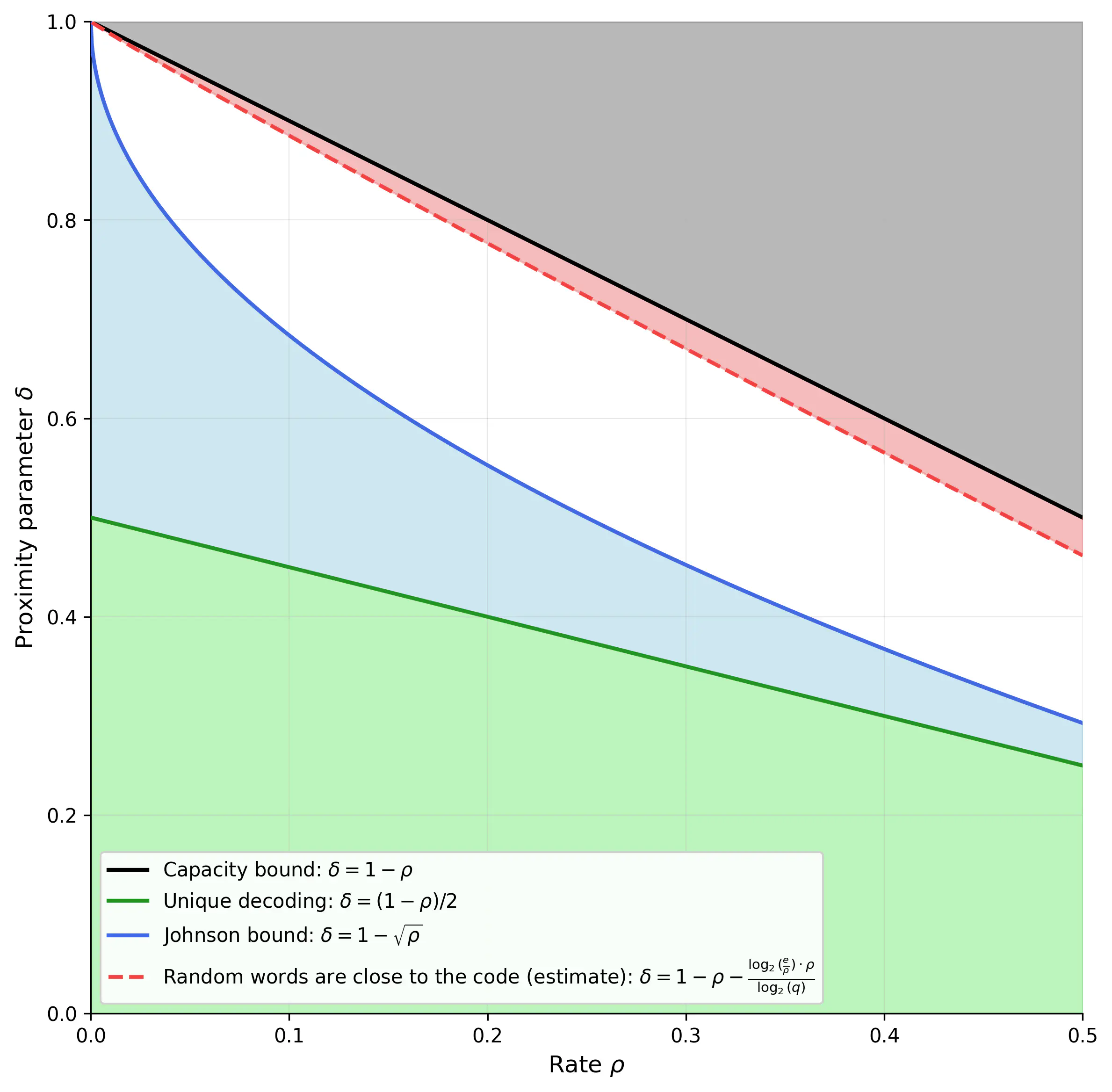
We’ll see how this affects our SNARKs a bit later. Before we do, let’s discuss what progress has been made for the rest of the white area.

Relating proximity gaps to other open problems

Although these papers do not explain the properties of the entire white area, they give us a sense of how hard the task will be. Both CS and BCHKS show that deciding the security status of the white area is as hard as a problem known as the “list-decoding” problem.

Roughly, this problem can be stated as follows: “if I send an encoded message over a noisy channel, how many errors can we tolerate while still being able to recover a small list of messages on the other end?”. Here small means a list size that is a polynomial function of the message length. This is an open problem.

The best known list-decoding algorithm corresponds exactly to the blue area of the graph. There is also a theoretical upper bound for list-decoding. We overlay this bound on our graph (see the yellow line below):

Let me highlight two important facts about this new yellow line. Firstly, and most importantly, it represents a new upper bound on the sets of parameters that are secure. Secondly, our graph shows it intersecting with the red area from the previous section. This is not to be taken as visual evidence; the red area drawn is just an approximation of the DG result. In practice, I am not sure how the yellow and red lines interact, especially because both lines depend on parameters beyond just $\rho$ and $\delta$.

Consequences for our SNARKs

The main consequence for our SNARKs is that we cannot set parameters to be above the yellow line or in the red area. Correcting this issue requires using a smaller value for $\delta$ and tuning the other parameters of the proximity test accordingly (for those familiar with proximity tests, I am referring to the number of queries). As we have seen, this means that prover time, verifier time and proof size will become larger.

How much larger depends on the new parameters chosen:

• if we want to be absolutely safe and operate in the proven-security region (i.e., not the white area), proof sizes will double. The verifier time will also roughly double. However, prover time will be mostly unaffected! This is because the prover’s computation is dominated by work that is proportional to $\rho^{-1}$, not $\delta$.
• if we want to keep operating in the unknown white area, then moving to the closest possible parameters will cause an increase in proof size and verifier time of up to 2-3%. As in the previous case, prover time will be mostly unaffected.

Conclusion

I’ll conclude by giving you some key takeaways:

1. hash-based SNARKs can operate in two parameter regimes: proven security or conjectured security. The former is certain to be secure but has worse performance.
2. some of the conjectured parameters were shown to not be secure.
3. a large area of unknown parameters remain.
4. adjusting our SNARKs to go from previously-conjectured security to proven security increases proof size and verifier time by 2x. The prover is mostly unaffected.
5. adjusting our SNARKs to go from previously-conjectured security to newly-conjectured security increases proof size and verifier time by 2-3%. The prover is mostly unaffected.