Mental Poker in the Age of SNARKs - Part 2
This article is cross-posted from the Geometry Notebook. The work was produced in collaboration with Andrija Novakovic and Kobi Gurkan for Geometry and MatchboxDAO.
In Part 1 of our Mental Poker series we highlighted the challenges of decentralised card games and presented the improved Barnett-Smart protocol as a practical solution. In this second part we take a deep dive into the cryptography that enables this protocol.
We will first inspect an instantiation of the verifiable $l$-out-of-$l$ threshold masking functions (VTMFs) using El Gamal encryption1. We will also show how repeated applications of these functions achieve the necessary properties for a fair card game. In the second section we cover the zero-knowledge argument for a correct shuffle as presented in “Efficient Zero-knowledge Argument for Correctness of a Shuffle”2.
Discrete-log VTMF (Mental Poker Revisited1)
A set of VTMFs is composed of 4 functions: key generation, mask, remask and unmask. These can be instantiated using a threshold variant of the El Gamal encryption scheme. Verifiability is achieved by computing zero-knowledge proofs that encryption and decryption are performed correctly.
✍️ Notation: We assume that players have agreed to use a finite abelian group $\mathbb{G}$ of prime order $q$. We denote $G$ the generator of $\mathbb{G}$ and use additive notation (”$+$”) for the group operation. We assume the existence of a public mapping $\mathcal{M}$ from card values to elements of $\mathbb{G}$; this could be a hash function for example. Given a card value, all players can compute $M = \mathcal{M}(\text{card})$ with $M \in \mathbb{G}$. The $\gets$ operator denotes an element chosen uniformly at random from a set, e.g. $X \gets \mathbb{G}$ In this section we will consider a group of $\ell$ players which we denote with the subscript $i \in \{1, 2, \dots, \ell\}$.
Key Generation
Player $i$ generates a private key $x_i \gets \mathbb{Z} _q$. The corresponding public key $H_i$ is computed as $H_i = x_i G$ and published.
To prevent rogue key attacks, we require that players prove in zero knowledge that they know the private key corresponding to the key they publish. In this discrete logarithm setting, such a proof is easily obtained using the Schnorr identification scheme.
Once all players have published their keys and proofs, an aggregate public key $H$ can be computed as:
$$ \begin{equation} H = \sum_ {i=1} ^\ell H_i = \sum_ {i=1} ^\ell x_i G \end{equation} $$
Mask
The mask function, denoted $\mathcal{E}_H$ when using the public key $H$, is in fact the El Gamal encryption of a card $M \in \mathbb{G}$. The resulting ciphertext $\mathbf{C} \in \mathbb{G} \times \mathbb{G}$ is a masked card.
$$ \begin{equation} \mathbf{C} = \mathcal{E}_H(M, r) = \left( \begin{array}{c} C_a \\ C_b \end{array} \right) = \left( \begin{array}{c} rG \\ M + rH \end{array} \right) \end{equation} $$
Here $r$, known as the masking factor, is an element of $\mathbb{Z}_q$ chosen uniformly at random by the player performing the mask operation. Notice that given a masked card and its corresponding masking factor, the plaintext card can be recovered without a secret key by computing $C_b - rH$. This would spell disaster for our scheme. As a consequence, masking factors must remain secret to protect a masked card’s hidden value.
Remask
The remask function, denoted ${\mathcal{E}_H}’$, allows to re-randomise a masked card $\mathbf{C} = \left( \begin{array}{c} C_a \\ C_b \end{array} \right)$. The player performing the remask operation chooses a random element $r’ \gets \mathbb{Z}_q$ and computes:
$$ \begin{equation} \mathbf{C’} = {\mathcal{E}_H}’(\mathbf{C}, r’) = \mathbf{C} + \left( \begin{array}{c} r’G \\ r’H \end{array} \right) = \left( \begin{array}{c} C_a + r’G \\ C_b + r’H \end{array} \right) \end{equation} $$
Example: using Mask and Remask to hide a card from all players
Let’s take a three player game as an example with Alice, Bob and Charlie respectively players 1, 2 and 3. Alice computes $\mathbf{C}_1$, the masking of card using the masking factor $\alpha$. Bob then computes $\mathbf{C}_2$ by remasking $\mathbf{C}_1$ using the masking factor $\beta$. Finally Charlie computes $\mathbf{C}_3$ by remasking $\mathbf{C}_2$ with the masking factor $\gamma$. Let us quickly run through the math to see what is actually happening:
$$ \begin{align} \mathbf{C}_1 &= \mathcal{E}_H(M, \alpha) = \left( \begin{array}{c} \alpha G \\ M + \alpha H \end{array} \right) \\ \mathbf{C}_2 &= {\mathcal{E}_H}’(\mathbf{C}_1, \beta) = \mathbf{C}_1 + \left( \begin{array}{c} \beta G \\ \beta H \end{array} \right) = \left( \begin{array}{c} (\alpha + \beta) G \\ M + (\alpha + \beta) H \end{array} \right) \\ \mathbf{C}_3 &= {\mathcal{E}_H}’(\mathbf{C}_2, \gamma) = \mathbf{C}_2 + \left( \begin{array}{c} \gamma G \\ \gamma H \end{array} \right) = \left( \begin{array}{c} (\alpha + \beta + \gamma) G \\ M + (\alpha + \beta + \gamma) H \end{array} \right) \end{align} $$
After every player has processed the card we are left with a masked card under the aggregate masking factor $\alpha + \beta + \gamma$: indeed notice that $\mathbf{C}_3 = \mathcal{E}_H(M, (\alpha + \beta + \gamma))$. Recovering the original card $M$ would require all players to share the masking factor they used or to participate in decryption.
Unmask
How can we untie the knot that was created above? We make use of the fact that a masked card (ciphertext) is composed of two group elements and each of these have had the same masking factors applied to them. Given a masked card $\mathbf{C} = \left( \begin{array}{c} C_a \\ C_b \end{array} \right)$ the $i$-th player can compute the value $D_i = x_i C_a$ using their private key. After each player publishes their value, the unmask operation can be performed as:
$$ \begin{equation} M = C_b - \sum_{i=1} ^\ell D_i \end{equation} $$
For those who want to see why this works: $$ \begin{align} C_b - \sum_{i=1} ^\ell D_i &= C_b - \sum_{i=1} ^\ell x_i C_a \\ &= (M + rH) - \sum_{i=1} ^\ell x_i (rG) \\ &= M + rH - r \sum_{i=1} ^\ell H_i \\ &= M \end{align} $$
Verifiability
Verifiability for the operations above (bar the key generation) is obtained by generating Chaum-Pedersen proofs of discrete log equality. In this classic $\Sigma$-protocol, a prover produces two values $\alpha G$ and $\beta H$ and proves in zero knowledge that they know $\alpha$ and that $\alpha = \beta$. A mask operation is verified using a Chaum-Pedersen proof for the values $C_a$ and $C_b -M$ with $\alpha = r$, remask using a Chaum-Pedersen proof for $C’a - C_a$ and $C’b - C_b$ with $\alpha = r’$ and finally decrypt using a Chaum-Pedersen proof for $G$ and $C_a$ using $\alpha = x_i$.
Zero-Knowledge Argument for Correctness of a Shuffle (Bayer-Groth2)
✍️ Notation: As we now consider actions on a deck of cards by a single player, we use subscripts to denote an item’s position in an array (rather than indicating a player as seen in the previous section).
Preliminaries
To understand the argument of a correct shuffle of ciphertexts, we will first look at shuffling a set of $N$ group elements $P_1, P_2, \dots, P_N$, each a member of $\mathbb{G}$. Each element $P_i$ is given a new index and some blinding $\Delta_i \gets \mathbb{G}$ is added. This blinding operation is the same as applying remask to one of the two elements in a masked card. We can express each point at the output of the shuffle $P’_i$ as:
$$ \begin{equation} P’_i = P _ {\pi(i)} + \Delta_i \end{equation} $$
where $\pi$ is a secret permutation. Below is a visual representation of the process for 6 elements. Can you write out the permutation that satisfies Equation (12)? (Answer in the image’s caption)
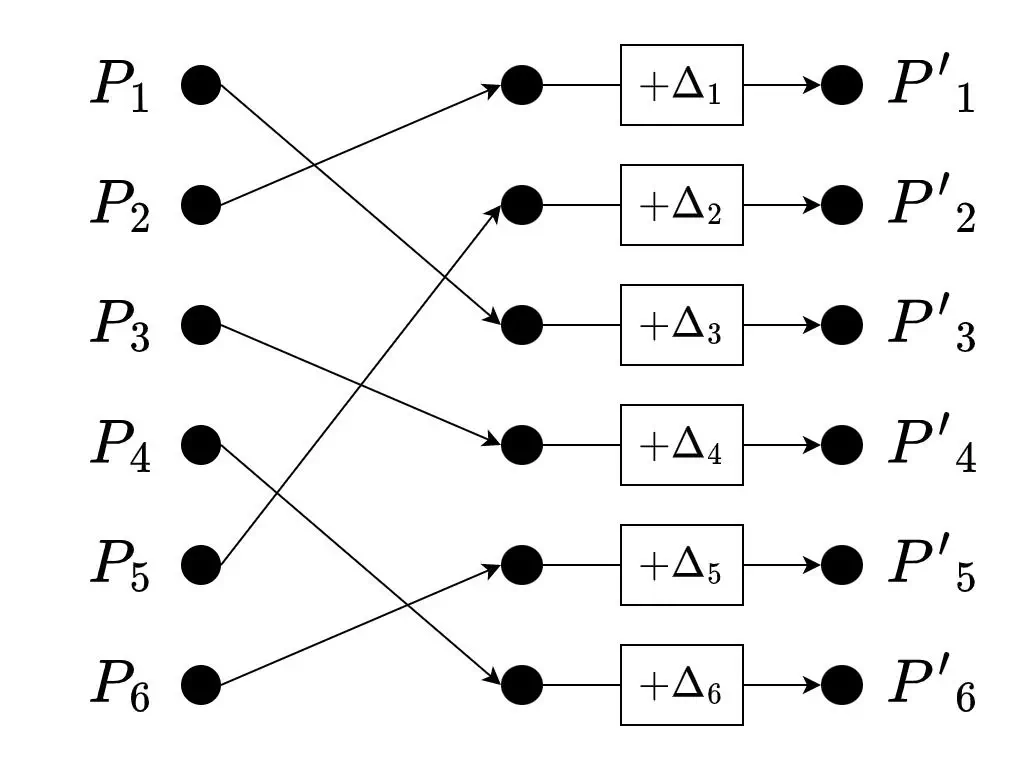
An example of a 6 point shuffle using the permutation π defined as π(1) = 2, π(2) = 5, π(3) = 1, π(4) = 3, π(5) = 6, π(6) = 4 . The permutation is read “backwards” on the diagram since equation 12 is indexed with respect to the output.
Argument Overview
In order to produce an efficient argument, we first express a correct shuffle in the form of a polynomial equality. Such equalities can be checked with an overwhelming degree of certainty by evaluating each polynomial at a randomly chosen point in the domain (see Schwartz-Zippel lemma). One of the polynomials will be computed by the verifier using public data, the other by the prover using secret data. Since the prover cannot be trusted, we must devise additional arguments to attest that the prover polynomial is computed correctly. We consider each of these steps separately in the sections below.
Shuffle as a Polynomial Equality
The core of the argument is the final verifier equation which we show below. For a fixed random challenge $z_c \gets \mathbb{Z}_q$, the verifier checks that:
$$ \begin{equation} \sum_{i=1} ^N {z_c}^i P_i = \sum_{i=1} ^N {z_c}^{\pi(i)} (P’_i - \Delta_i) \end{equation} $$
The left-hand side of this equation uses only public data (the shuffle’s inputs) and our random scalar; it can therefore be computed by the verifier. The right-hand side however can only be evaluated by the prover as it requires knowledge of the secret permutation $\pi$ and blinding elements $\Delta_i$.
The first thing we should notice is that these expressions are very similar to the evaluation of two polynomials at the input $z_c$. The underlying polynomials can be made apparent by rewriting our elements $P_i$, $P’_i$ and $\Delta_i$ as the product of some scalar and a generator. For all $i$ in $\{ 1, 2, \dots, N\}$, let
- $s_i \in \mathbb{Z}_q$ such that $P_i = s_i G$
- $s’_i \in \mathbb{Z}_q$ such that $P’_i = s’_i G$
- $\delta_i \in \mathbb{Z}_q$ such that $\Delta_i = \delta_i G$
Substituting the above into Equation (13) and factoring out of the sum we can rewrite the verification equation as:
$$ \begin{equation} \left( \sum_{i=1} ^N {z_c}^i s_i \right) G = \left( \sum_{i=1} ^N {z_c}^{\pi(i)} (s’_i - \delta_i) \right) G \end{equation} $$
Consider the polynomials $f$ and $g$ described below and notice that the above expressions correspond to these polynomials evaluated at $z_c$ and multiplied by our group generator:
$$ \begin{equation} f(z) = \sum_{i=1} ^N z^i s_i \quad \text{ and } \quad g(z) = \sum_{i=1} ^N z^{\pi(i)} (s’_i - \delta_i) \end{equation} $$
Given that sums are commutative, we can rewrite $f$ as $f(z) = \sum_{i=1} ^N z^{\pi(i)} s _ {\pi(i)}$: we simply change the order of the terms in the sum. This now makes it apparent that:
$$ \begin{align} f(z) = g(z) &\iff \sum_{i=1} ^N z^{\pi(i)} s _ {\pi(i)} = \sum_{i=1} ^N z^{\pi(i)} (s’_i - \delta_i) \\ &\iff \forall i \in \{1, 2, \dots, N \}, s _ {\pi(i)} = s’_i - \delta_i \\ &\iff \forall i \in \{1, 2, \dots, N \}, P _ {\pi(i)} = P’_i - \Delta_i \end{align} $$
Or put into words, the polynomials $f$ and $g$ are identical if and only if the shuffle is valid.
Checking the Polynomial Equality
To check the polynomial equality, we evaluate both polynomials at a point $z_c \gets \mathbb{Z}_q$ and check that $f(z_c) = g(z_c)$. While this does not guarantee that the polynomials are identical, it allows us to assert it with probability $1 - \frac{N}{|\mathbb{Z}_q|}$ (see Schwartz-Zippel lemma), where $|\mathbb{Z}_q| > > N$.
Notice also that we do not have access to the values $s _ {\pi(i)}$, $s’_i$ and $\delta_i$ but instead can only use $P _ {\pi(i)}$, $P’_i$ and $\Delta_i$. Therefore we must evaluate the polynomials “in the exponent” as made explicit by Equation (14).
Ensuring the Prover Behaves Honestly
As mentioned previously, the right-hand side of the verification equation, $\sum_{i=1} ^N {z_c}^{\pi(i)} (P’_i - \Delta_i)$, must be computed by the untrusted prover without revealing any private information. We reconcile both these requirements with commitments and zero-knowledge arguments.
First the prover will commit to a permutation and will show in zero knowledge that they permuted powers of the challenge $z_c$ according to the committed permutation (permutation argument). After running such an argument, the verifier will hold a commitment $C _ {z, \pi}$ which binds the prover to the vector $\left[z_c ^ {\pi(1)}, z_c ^ {\pi(2)}, \dots, z_c ^ {\pi(N)} \right]$ . This vector can now be used in an inner-product argument to produce a provable evaluation of the expected sum: $\sum_{i=1} ^N {z_c}^{\pi(i)} (P’_i - \Delta_i)$.
These arguments are not trivial and probably require their own articles to present a solid intuitive and mathematical understanding. A potential extension of the series? Who knows… In the meantime, a bit of ZK trivia: both the inner-product argument and permutation argument presented in “Efficient Zero-knowledge Argument for Correctness of a Shuffle”2 were later adapted and improved to respectively form part of Bulletproofs and PlonK.
From Shuffling Group Elements to Shuffling Cards
Recall that all the above only concerns shuffling a single group element rather than a masked card (a ciphertext composed of two group elements). We can however extend the above reasoning to masked cards in either of two ways:
- Run the argument for elements twice and request that the prover use the same committed permutation for both sets of group elements. This is naturally feasible with the existing argument structure as the prover is already required to commit to a permutation and argue that it was used correctly.
- Consider each masked card as an element of the group $\mathbb{H} = \mathbb{G} \times \mathbb{G}$ and define the group operation for $\mathbb{H}$ to remain consistent with how we add ciphertexts in our remask formula.
Implementation
All the protocols described in this article were implemented in an open-source Rust library by Andrija Novakovic, Kobi Gurkan and yours truly as part of the collaboration between Geometry and MatchboxDAO. The implementation relies on the arkworks ecosystem and is built to be highly modular. Indeed the arguments can be replaced in a “plug-and-play” manner while the protocols are implemented for any generic curve. As you might have noticed, these protocols do not require special operations such as pairings or FFTs and can therefore be run on any elliptic curve.
We benchmarked the library on a STARK-friendly curve (used by StarkWare), running on consumer hardware. A shuffle argument for 52 cards, complete with the remasking of the cards, takes about 50ms. Verification of a shuffle can be done in less than 1ms. Note however that a game is only guaranteed to be fair after all players have taken turns performing this shuffle operation.
Conclusion
In this article we have reviewed the principal results of Mental Poker Revisited1 and Efficient Zero-knowledge Argument for Correctness of a Shuffle2. While we have not covered all the mechanics of the shuffle argument, we have presented the reader with a global overview of the protocol’s steps and justification as to why the protocol correctly verifies a shuffle.
Combining both results yields the efficient protocol for card games that we described in Part 1 of our Mental Poker series. Our Rust implementation of the protocol in collaboration with MatchboxDAO is available here; decentralised games will hopefully be coming soon!
-
Barnett, Adam, and Nigel P. Smart. “Mental poker revisited.” In IMA International Conference on Cryptography and Coding, pp. 370-383. Springer, Berlin, Heidelberg, 2003. ↩︎ ↩︎ ↩︎
-
Bayer, Stephanie, and Jens Groth. “Efficient Zero-knowledge Argument for Correctness of a Shuffle.” In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pp. 263-280. Springer, Berlin, Heidelberg, 2012 ↩︎ ↩︎ ↩︎ ↩︎