Mental Poker in the Age of SNARKs - Part 1
This article is cross-posted from the Geometry Notebook. The work was produced in collaboration with Andrija Novakovic and Kobi Gurkan for Geometry and MatchboxDAO.
Is it possible to play a classic card game without physical cards, without trusting the participants and without a trusted third party?
This problem was first formulated and given the name “Mental Poker” in 1979 by none other than Rivest, Shamir and Adleman1. Below is an extract from the original paper in which they explain the notion of Mental Poker.

Since then, many solutions have been published but none were deemed practical. These protocols incurred computation and communication costs that were too large for a game to be played in real-time. Today with the advent of decentralised ledgers, zero-knowledge rollups and efficient SNARKs, we believe that it is time to revisit Mental Poker once again.
In this first of two articles we will cover existing solutions and our improvements towards making such protocols practical. We look at Mental Poker from a high level with an emphasis on understanding the cryptographic primitives at work and how they interact. In Part 2 we will open Pandora’s box and closely inspect the mathematics and cryptography.
We implement the protocol described here in a Rust library as part of the collaboration between Geometry and MatchboxDAO (see source code). Our naive implementation for a 52-card deck allows a player to produce a proof of correct shuffle (the most expensive operation) in just over 50ms on a standard laptop, with verification requiring less than 1ms. Note however that a game is only guaranteed to be fair after all players have taken turns performing this shuffle operation.
Problem Overview
The main challenges in creating a protocol for Mental Poker are:
- hide the card values from all players
- reveal a card to a specific player or group of players
- ensure that the cards are dealt correctly, with fair randomness
Some additional desirable properties include the ability to keep some information secret after the game ends - effectively allowing for bluff strategies - and the possibility to add or remove players to a game.
To these requirements we must add performance considerations. How much data do we need to store for each card? How many messages does each player need to send/receive? What kind of computations do players need to run?
Geometry revisits Mental Poker
Related Work
The most noteworthy solutions in the literature are A Toolbox for Mental Card Games (Schindelhauer, 1998)2, its implementation in a C library (Stamer, 2005)3 and a revised approach presented in Mental Poker Revisited (Barnett and Smart, 2003)4. While these protocols work on paper they were deemed impractical due to large computation or communication costs. Other approaches focus on the game of poker specifically5 (as opposed to general card games), introduce a partly trusted party5 or require trusted execution environments6.
We choose to focus on the protocol by Barnett and Smart for multiple reasons. Firstly, the security of their protocol relies on the well known Decisional Diffie-Hellman assumption. Secondly, the protocol is built on top of clear and logical abstractions which allow for easy “plug-and-play” improvements. Finally the computation and communication costs of their protocol are dominated by zero-knowledge proofs: an area in which we have seen great performance improvements since the paper was published in 2003.
The Improved Barnett-Smart Protocol
The Barnett-Smart protocol relies on two cryptographic abstractions. Operations on cards are performed using a set of verifiable $l$-out-of-$l$ threshold masking functions. Quite a mouthful - we will explain these in the following section. The second abstraction allows to perform operations on a deck and is known as a zero-knowledge proof of a correct shuffle. Also a mouthful but a less cryptic one.
The masking functions described in the original paper make use of a threshold variant of the well-known El Gamal encryption scheme. This scheme can be instantiated over elliptic curves to provide high security while maintaining a compact representation for cards (each card is represented by two elliptic curve points). On the other hand, the shuffle proof presented by Barnett and Smart did not withstand the test of time. Today much cheaper and quicker schemes are available. Our improvement lies in replacing the original zero-knowledge proof by a zero-knowledge argument - more on this distinction later.
Verifiable $l$-out-of-$l$ Threshold Masking Functions
Verifiable $l$-out-of-$l$ threshold masking functions (VTMFs) were introduced by Barnett and Smart to abstract away from specific implementation details. We will only focus on what they describe as a “discrete-log VTMF”. First let us break down the name into digestible terms:
- masking: these functions allow us to “mask” or hide a piece of data. In this sense, encryption is a form of masking.
- verifiable: an observer should have the ability to check that a masking function was applied correctly, even if the function requires some secret information to be ran.
- $l$-out-of-$l$ threshold: some of these functions will require a given threshold of participants to be ran. In this case the threshold is set to the number of participants ($l$-out-of-$l$), effectively requiring that all players collaborate.
Combining these three properties, VTMFs will allow us to hide card values (masking) while guaranteeing that no individual player is cheating (verifiable) nor can a coalition of players cheat ($l$-out-of-$l$ threshold). The functions are: key generation, mask, remask and unmask. We cover each of these individually.
Key Generation
Each player is expected to run a key generation algorithm which outputs a secret key and a public key. For player $A$, we denote the secret key $\mathsf{sk}_A$ and the public key $\mathsf{pk}_A$. Each player publishes their public key along with a zero-knowledge proof that they know the corresponding secret key. This proof is necessary to prevent denial-of-service attacks and rogue key attacks.
Once each player has completed the above process, an aggregate public key, $\mathsf {pk}_ {Agg}$, can be computed. While there exists in theory an aggregate secret key that corresponds to $\mathsf{pk}_ {Agg}$, this secret key will remain unknown to all parties as long as at least one player keeps their secret key hidden. The figure below illustrates this key aggregation process.
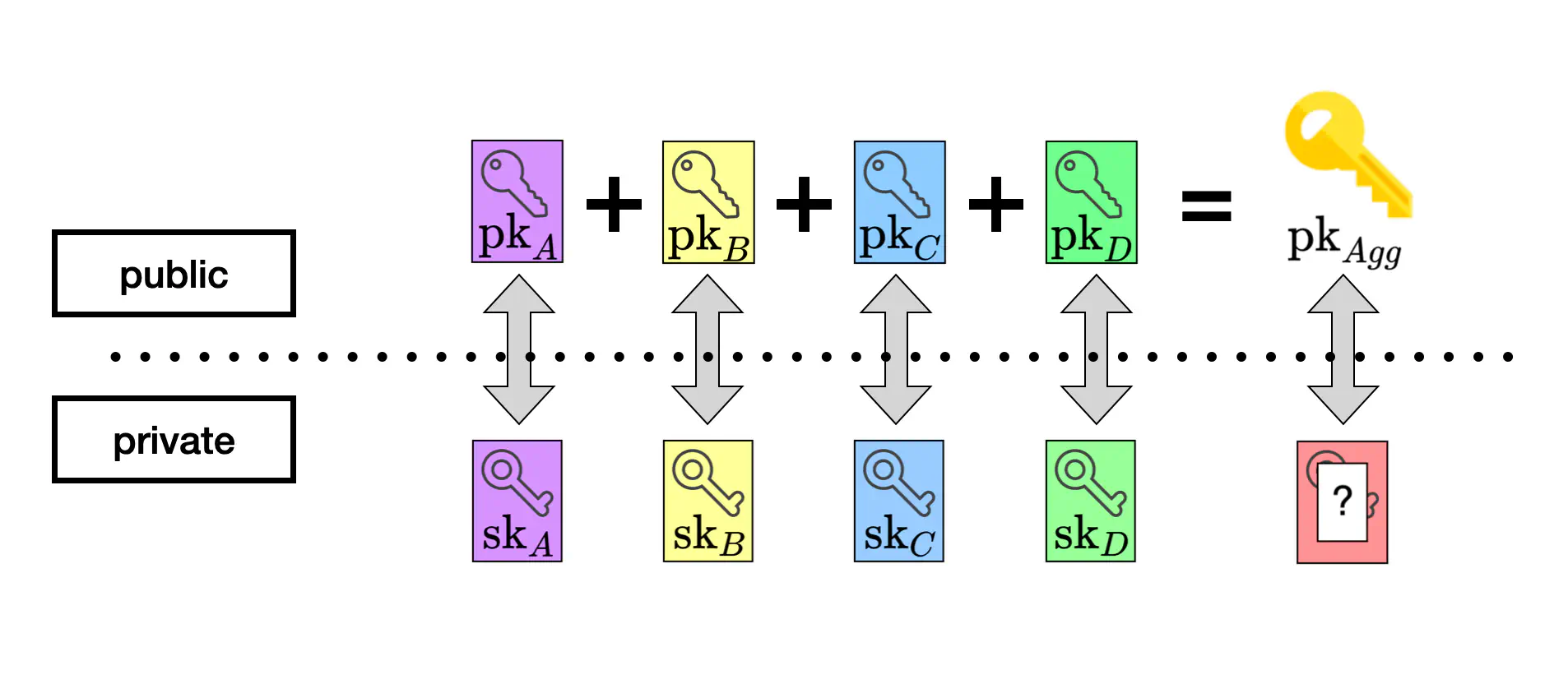
An illustration of a 4-player key aggregation. Importantly, no one can derive the secret key that corresponds to the aggregate public key.
Mask
A mask operation is an encryption. A plaintext card is processed along with the aggregate public key and some randomness to produce a ciphertext: the masked card. To recover the plaintext card, one must decrypt (unmask) the masked card. As we will see, this process can only be performed by a coalition of all players.
A good mental model is to picture a masked card as an opaque box with a set of padlocks on it. Each padlock can be opened by one of the players’ secret key. Notice however that each ciphertext is unique: this is akin to having a label on the box. The figure below illustrates this mental model.
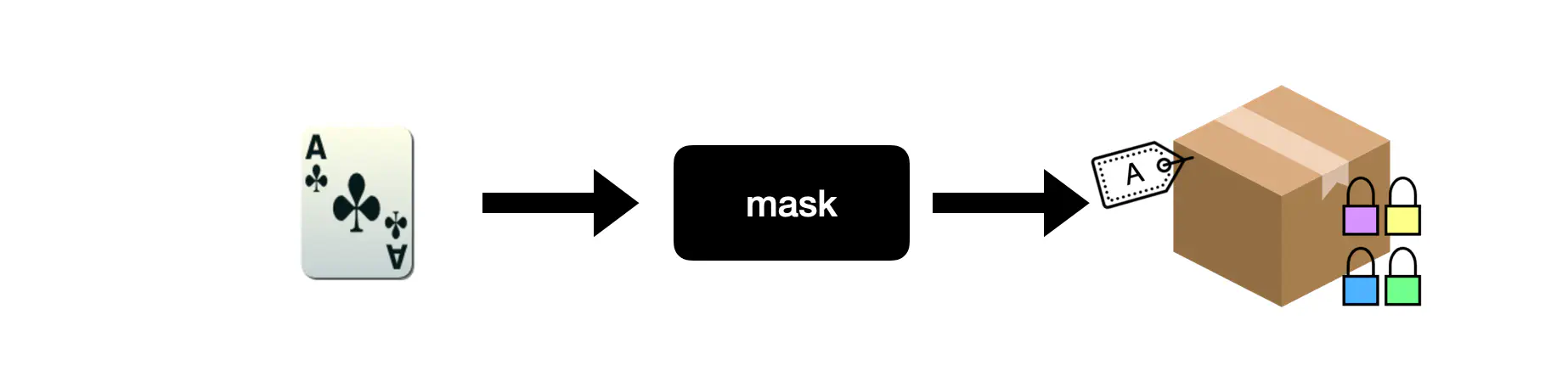
A mask operation can be understood as placing a card in an opaque box with padlocks for each player and a label.
Masking alone does not guarantee a fair game. Indeed the player who performed the mask operation will be able to maintain a mapping from card value to box label. In the above example the ace of clubs maps to the label “A”. To break this mapping, we introduce the remask operation.
Remask
A remask operation takes a masked card (ciphertext) and produces a new masked card for the same underlying card value (plaintext). This operation does not require to decrypt the ciphertext and therefore can be performed by any player. To follow our box analogy, a remask operation just replaces the label on a box.
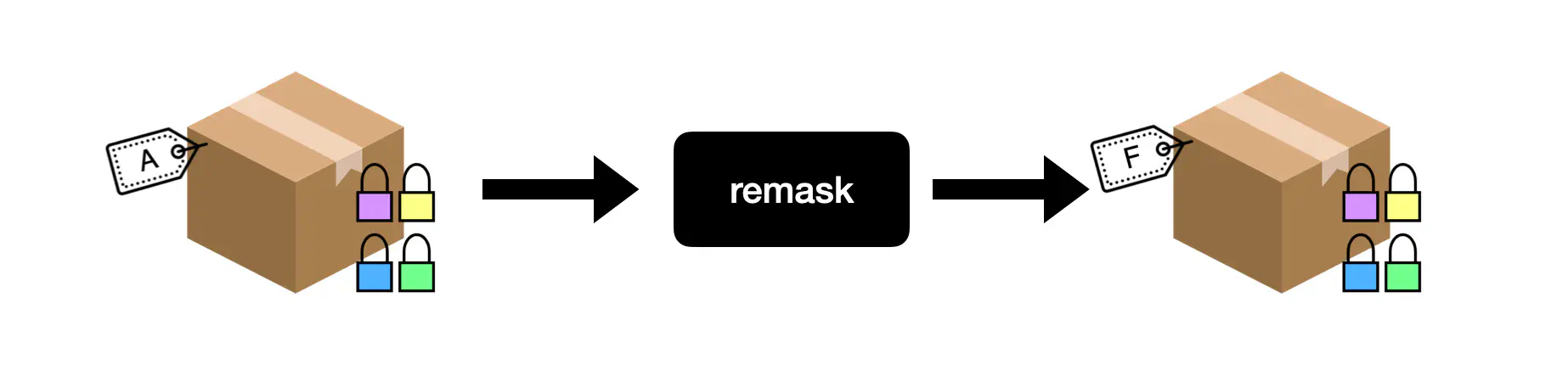
A remask operation can be understood as re-labelling a box (masked card).
Unmask
The unmask operation is a threshold decryption. Each player must use their secret key to contribute to the decryption. Crucially, this group decryption can be performed in stages. This allows to give out cards to specific players. For example players $A$, $B$ and $C$ can perform their part of the unmasking process such that the resulting ciphertext can be decrypted by player $D$ alone. Player $D$ can now decrypt the card in private and will be the only one to know its value.
To complete our box analogy, unmasking allows each player to remove their padlock from a box.
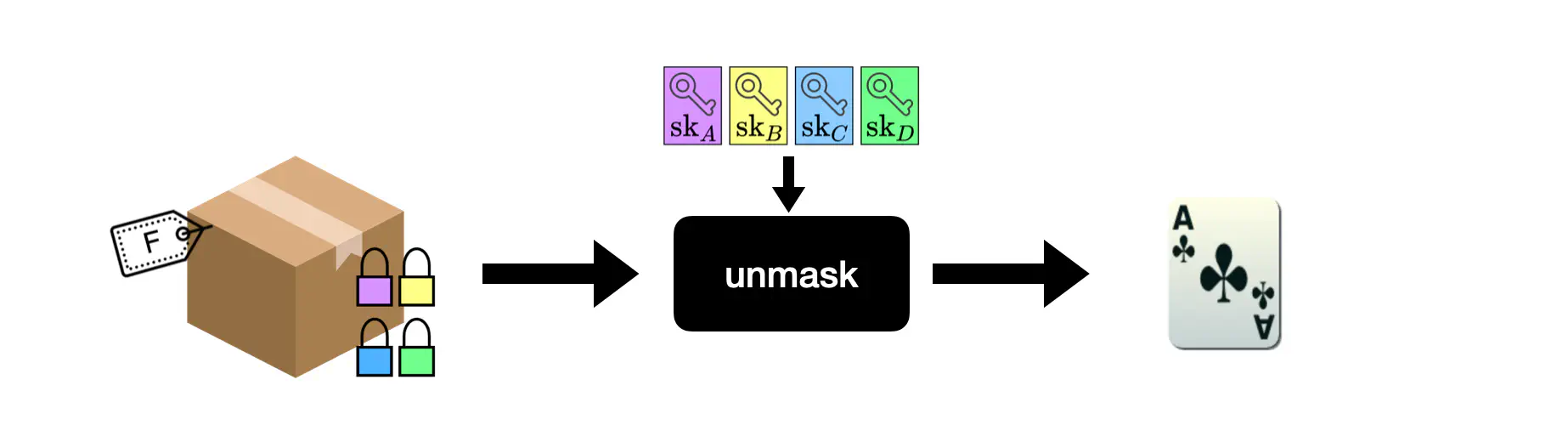
An unmask operation requires every player to use their secret key to remove their padlock from a box.
Zero-knowledge Argument of a Correct Shuffle
In this model, a shuffle is obtained by changing the order of a deck of masked cards and remasking them. Indeed recall that each masked card is uniquely identifiable, as opposed to a physical card that has been flipped. Simply changing the order of masked cards would not hide any information. Performing an additional remask allows to truly “lose” the cards in the deck.
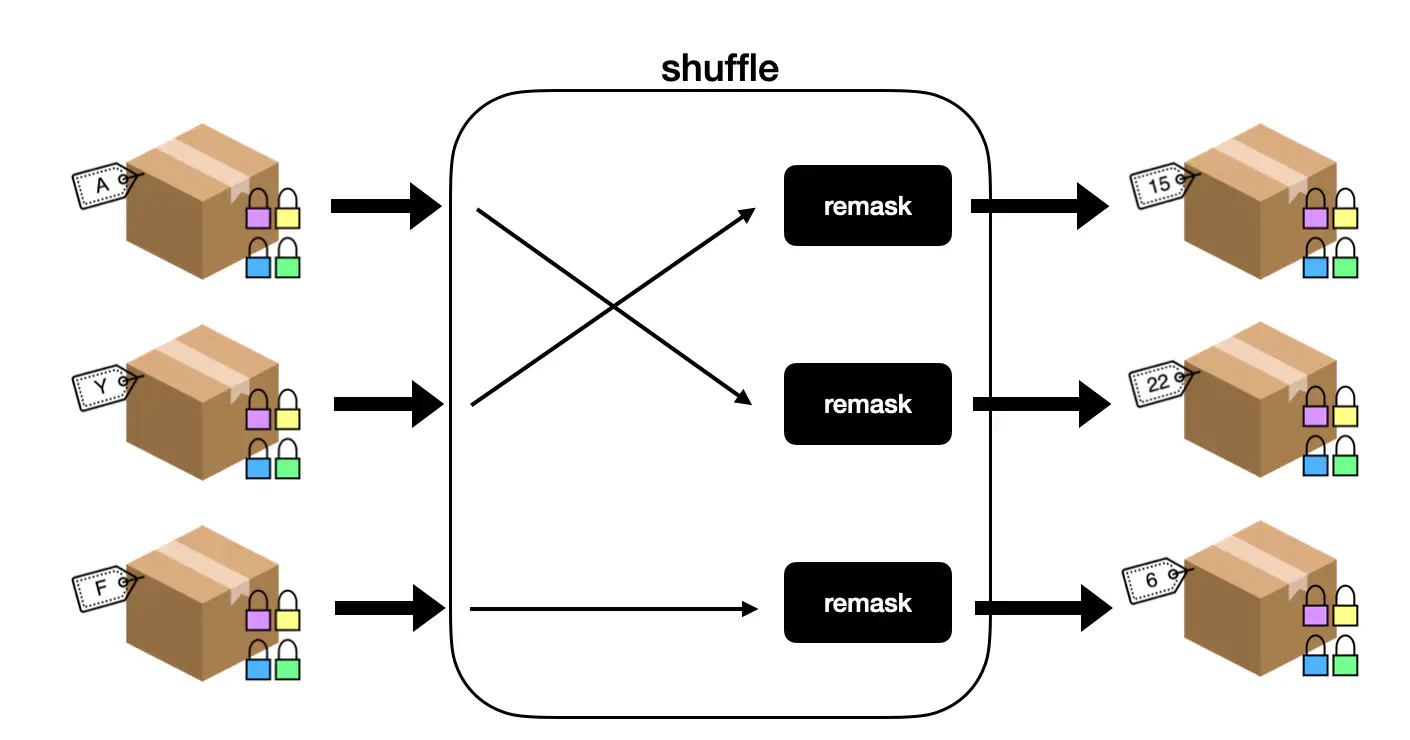
An illustration of a shuffle: we apply a permutation to the input masked cards and remask them.
The original protocol from Barnett and Smart produces a zero-knowledge proof to attest that this operation was computed correctly. This proof is expensive to compute as it requires the prover to perform a large number of shuffles, and therefore a large number of remask operations. Instead we replace the proof by an argument of knowledge.
An argument is cheaper to compute but yields slightly weaker security. While a valid proof can never be forged by a malicious prover, a valid argument can be forged by a sufficiently powerful adversary. Therefore, an argument is only meaningful under the assumption that the adversary is computationally bounded. Notice however that other cryptographic primitives such as public key encryption also share this property.
Today, there exists an incredible variety of arguments of knowledge that could be used to prove a correct shuffle: universal SNARKs (e.g. Marlin, PlonK), circuit-specific SNARKs (Groth16) and inner-product arguments (Bulletproofs, Bayer-Groth) to list a few. All of these are valid choices. We differentiate them based on the operations they require, any potential setups, the size of an argument, and running time for the prover and verifier.
The setting for Mental Poker is very different to the usual SNARK setting. First notice that we are dealing with a small number of participants that will all be online at the same time. In this case, the infamous trusted setup becomes a respectable option. Secondly, our input sizes are relatively small. A classic deck of cards is composed of 52 cards; other games rarely use more than a few hundred. In these ranges, computations that run in $\mathcal{O}(\sqrt{n})$ steps and $\mathcal{O}(\log(n))$ steps are relatively similar. The same reasoning applies for proof sizes.
To build our proof-of-concept code, we chose to prioritise arguments with no special requirements for the underlying curve (no need for pairings or FFTs) and with simple implementations. Based on these criteria we used the argument presented by Bayer and Groth in Efficient Zero-Knowledge Argument for Correctness of a Shuffle (2014)7. We stress however that any of the options mentioned above would yield a functioning and efficient protocol.
An example round of Texas Hold’Em
The table below presents an example round of Texas Hold’Em, showing on the left the actions that players would take in the classic (physical) version of the game, and on the right the digital equivalents.
Setup
| Texas Hold’Em | Mental Texas Hold’Em | |
|---|---|---|
| 1. | Gather a group of players around a table | Players each run the key generation algorithm, publish their public key and prove in zk that they own the corresponding secret key. A master public key is computed. |
| 2. | Bring a deck of 52 standard cards. Publicly encode each card value to a card (plaintext). | Mask all 52 cards with a public randomness value and publish all proofs. |
Round $n$
| Texas Hold’Em | Mental Texas Hold’Em | |
|---|---|---|
| 3. | Dealer shuffles the deck. | All players take turns running a shuffle and provide a zero-knowledge proof. |
| 4. | Give out the cards: top card goes to the first player, second card goes to second, etc… | Take part in the unmask process to allow players to see their cards: all players but the first partially unmask the first card, all players but the second partially unmask the second card, etc… |
| 5. | Betting using physical chips. | Betting using physical chips. |
| 6. | Discard and reveal cards using the game rules. | Following the order of the deck, ignore discarded cards. To open a card, all players collaborate to perform a full unmask of the chosen card. |
| 7. | Repeat 5 and 6 as mandated by the rules. | Repeat 5 and 6 as mandated by the rules. |
| 8. | Final betting. Open hands and declare a winner. | Final betting. Each player can complete the unmask process for their private cards. Compare hand values and declare a winner. |
Benefits of On-chain Coordination
One final aspect in which we can improve the existing protocols is to make use of decentralised ledgers and smart contracts running on top of them. The Barnett-Smart protocol already requires “a broadcast channel between all players”. A smart contract can be seen as an extension of such a broadcast channel where the channel itself can perform some computation.
In this context, we can delegate all the proof verifications to the smart contract: rather than having every player run a verifier for every proof, we only need one verification of each proof. The code for the smart contract is public and can therefore be audited by all players if they wish so. A particularly distrusting player can still choose to verify the proofs themselves.
Furthermore, a multi-round betting game like poker benefits greatly from the payment security offered by decentralised ledgers. Research such as this paper by Kumaresan et al. consider incentive and slashing mechanisms to force players to behave honestly.
To be continued…
In this first article we have covered the Barnett-Smart protocol for Mental Poker as well as our improvement to make the protocol practical. In Part 2 we show how and why the cryptography works.
-
A. Shamir, R. Rivest, and L. Adleman, “Mental Poker”, Technical Memo LCS/TM-125, Massachusetts Institute of Technology, April 1979. Link to paper. ↩︎
-
Schindelhauer, C. A Toolbox for Mental Card Games. Tech. Rep. of Medizinische Universitat Lubeck. ↩︎
-
Stamer, H. Efficient Electronic Gambling: An Extended Implementation of the Toolbox for Mental Card Games. WEWoRC 2005, LN P-74, 1-12, 2005 ↩︎
-
Barnett, Adam, and Nigel P. Smart. “Mental poker revisited.” In IMA International Conference on Cryptography and Coding, pp. 370-383. Springer, Berlin, Heidelberg, 2003. ↩︎
-
Golle, P. Dealing Cards in Poker Games. In Proceedings of the International Conference on Information Technology: Coding and Computing, (2005) ↩︎ ↩︎
-
Castellà-Roca, J., Domingo-Ferrer, J., Sebé, F. (2006). A Smart Card-Based Mental Poker System. In: Domingo-Ferrer, J., Posegga, J., Schreckling, D. (eds) Smart Card Research and Advanced Applications. CARDIS 2006. Lecture Notes in Computer Science, vol 3928. Springer, Berlin, Heidelberg. Link to paper. ↩︎
-
Bayer, Stephanie, and Jens Groth. “Efficient zero-knowledge argument for correctness of a shuffle.” In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pp. 263-280. Springer, Berlin, Heidelberg, 2012 ↩︎