Highlights of libZK, the Google Wallet ZKP
Last month, Google announced an update to Google Wallet that enables “fast and private age verification’’. As you might expect, the system uses zero-knowledge proofs (ZKPs) under the hood. This is great news! Firstly because these privacy-preserving primitives will get wider distribution and hopefully adoption. Secondly because it’s great to see high-performance, production-grade ZKPs being developed outside of the blockchain/web3 industry. And finally because seeing governments and big tech players like Google take interest in ZKPs is a clear sign of momentum for our beloved privacy-enhancing technologies.
The anonymous credential protocol is an implementation of the Anonymous credentials from ECDSA paper by Matteo Frigo and Abhi Shelat.
The underlying ZK proof system and implementation techniques are also documented in an IETF draft under the name libZK.
In this post, I wanted to highlight some innovations, observations and insights that went into the libZK proof system that I think we — the “ZK community” — should all pay attention to and learn from.
The post is not a full explainer or tutorial on the proof system, rather I hope that it serves as a teaser and motivates you to read the paper, or listen to an upcoming ZKPodcast episode where we interview Matteo and Abhi.
Below is a quick overview of the discussion points, organized into four categories. The rest of the article expands on this summary and discusses each point further.
Highlights of libZK.
- Proof system:
- similarly to our “client-side proving” trend,
libZKprioritizes a fast prover and concretely small proofs over asymptotic proof size and verifier time.- the proof system uses proof composition to reduce commitment costs (using a GKR-like inner proof) and preserve the zero-knowledge property (using a Ligero outer proof).
- the proof system composes interactive proofs (IPs) rather than SNARKs to avoid arithmetizing Fiat-Shamir challenges and allow for a cleaner security proof.
- Arithmetization:
- the system proves a “dual-circuit aritmetization”; some constraints are defined over the base field of the secp256r1 curve (useful for verifying ECDSA signatures) while others are defined over a 16-bit binary field (useful for verifying SHA-256 and parsing binary formats such as JSON or CBOR).
- the dual-circuit paradigm requires additional constraints to ensure that witness values remain consistent across the two circuits; this is done by computing a MAC inside each circuit and comparing it to a public input.
- Implementation techniques:
- the Ligero outer proof requires to encode the witness using a Reed-Solomon code. Instead of using the usual interpolate-and-evaluate method,
libZKencodes by computing a convolution. This can be computed in $\mathcal{O}(n \log n \log\log n)$ field-operations in any field using Nussbaumer’s algorithm; or in $\mathcal{O}(n \log n)$ field-operations if FFTs are available.- when using field extensions, the convolution technique allows to choose RS codes where the interpolation and evaluation domains are in the small subfield. This reduces proof size by a constant factor.
- FFTs can be computed in the quadratic extension of the base field of secp256r1 for a minimal overhead (a technique that first appears in Virgo and was later adopted by Circle STARK).
- FFTs can be computed in binary fields using the additive FFT, a technique also used in Binius.
- Circuit design:
- the inner proof system is GKR-like and therefore requires “layered” circuits. The circuit depth for CBOR parsing is kept low by using parallel-prefix techniques that are well-known (according to the authors) in the hardware world.
Proof system
Prioritize prover time above all else
The libZK system in designed for the use case of smartphone-generated anonymous credentials — or as we like to call it, “client-side proving”.
The main constraints are device power and bandwidth: the former requires the ZKP to be prover-efficient, while the latter requires that the proofs are concretely small-ish.
Similarly to the trends we have seen in our space, these constraints push us towards systems that:
- commit to as little data as possible,
- have efficient provers and
- avoid expensive “public key” operations.
Requirements 1 and 2 point us towards sumcheck-based proof systems and in particular GKR-like systems to minimize commitment costs. Requirement 3 usually directs us towards proof systems that only rely on hash functions.
The question then become: how do we efficiently add zero-knowledge to a GKR-like, hash-based proof system?
The answer in libZK is by composing the GKR-like proof with the Ligero ZKP.
Note that this is the full Ligero ZKP, not just the polynomial commitment scheme.
Another important point to notice is that the composition allows for an overall protocol that is cheaper than running Ligero alone. Indeed, in Ligero we would need to express the statement as an R1CS circuit and commit to the full R1CS witness, including any intermediate variables that exist in the circuit. On the other hand, by using GKR and composition, the prover only needs to commit to the GKR witness (much smaller!) and some additional random masking as we will see in the next section. Overall, Frigo and Shelat report a 20x improvement in prover speed over running Ligero alone.
Composing IPs not SNARKs
Typically when we do proof composition, we do so at the non-interactive argument level. Concretely, we generate an inner SNARK by taking an interactive protocol and making it non-interactive using the Fiat-Shamir transform1. We then generate an outer proof for the statement “the verifier of the inner SNARK accepts”. Doing so requires to arithmetize the full verification process of the SNARK, including the derivation of Fiat-Shamir challenges.
Instead, libZK composes the GKR protocol and Ligero as interactive proofs (IPs).
It also adds a layer of masking of the GKR transcript in order to make the full protocol zero-knowledge.
You can get an idea for how this composition is performed by looking at the figure below.
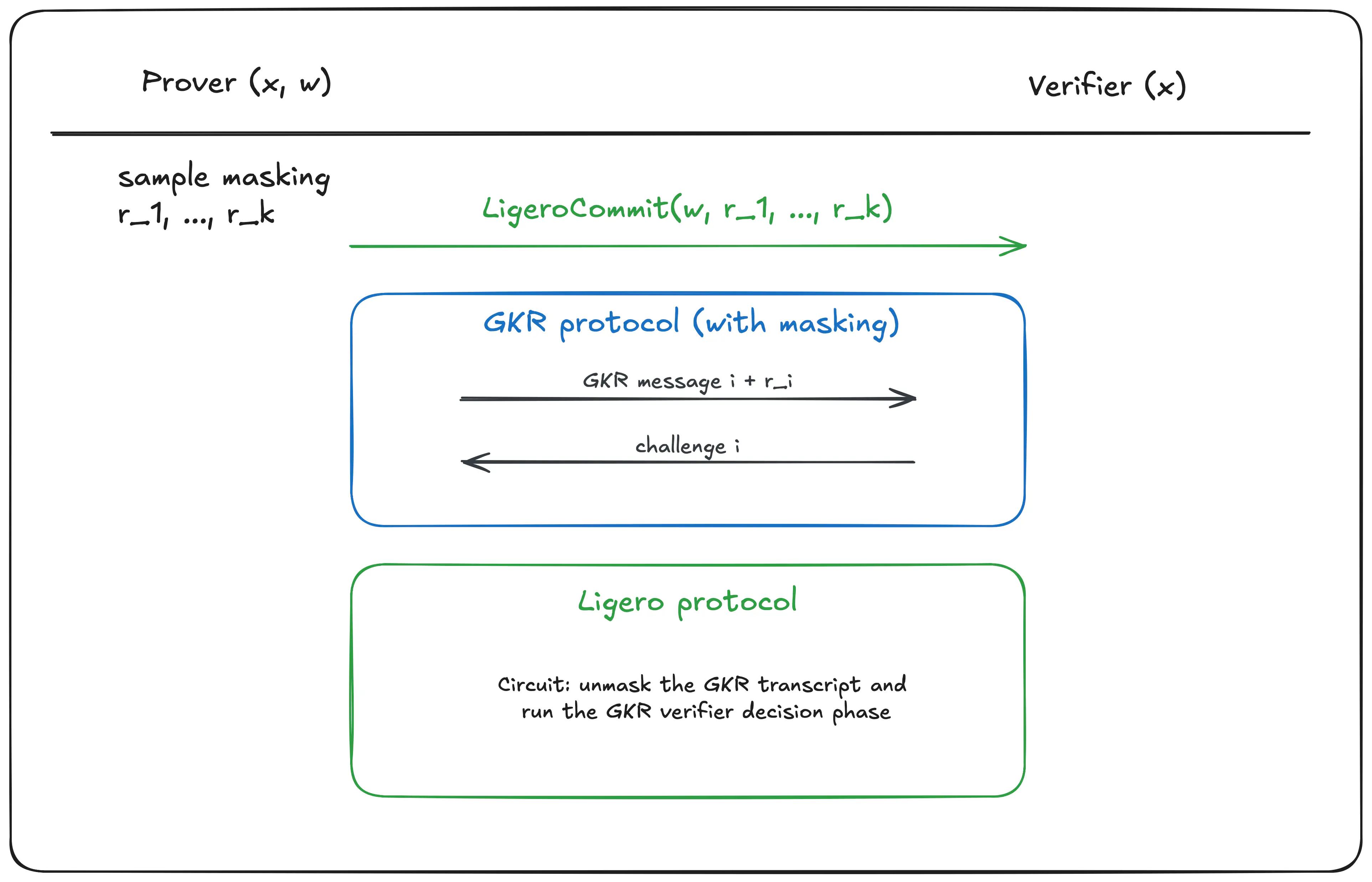
Overview of the composed interactive protocol.
There are two main benefits to composing IPs rather than SNARKs:
- the outer proof circuit does not need to enforce constraints for the correct derivation of Fiat-Shamir challenges.
- the protocol can be proven secure either as an interactive proof in the standard model, or non-interactive proof in the ROM. This is usually not possible when we compose SNARKs.
As always, the interactive protocol described above can be made non-interactive by applying the Fiat-Shamir transform.
The downside, however, is that we do not get the “proof compression” effect that SNARK composition provides. Indeed, by composing IPs in this way, the transcript of the full protocol is a concatenation of the GKR and Ligero transcripts. After applying Fiat-Shamir, we are left with a non-interactive proof that is the collection of the inner and outer protocol messages, rather than simply the outer protocol messages as would be the case in SNARK composition.
Dual-circuit arithmetization
Choice of fields
Due to its use in anonymous credential systems, libZK is geared towards verifying ECDSA signatures and parsing the signed message.
Standard ECDSA signatures are computed over the curve secp256r1 for which the base field is a prime field of characteristic $p$: $$p := 2^{96} * 7 * 274177 * 67280421310721 * 11318308927973941931404914103 - 1.$$
Choosing to enforce constraints using a circuit over $\mathbb{F}_p$ allows to express the ECDSA verification algorithm in very few constraints.
However, ECDSA signatures also require a SHA-256 hash of the signed message.
Furthermore, the messages used by the anonymous credential system are often serialized in the CBOR format; a JSON like format for binary data.
Verifying the hash and parsing the CBOR message are therefore mostly bit- or byte-wise operations.
Inspired by Binius, libZK makes use of a 16-bit binary field to efficiently enforce these constraints.
Note that libZK does not use a tower of binary fields like Binius and the comparison is left as future work by the authors.
Using MACs for cross-circuit consistency
The downside of using two circuits is that the proof system needs to ensure that those circuits are linked and that even if witness values are represented differently in each circuit, they remain consistent.
The solution in libZK is to augment both circuits to compute a message-authentication code (MAC) on the shared witness elements inside each circuit.
These in-circuit MACs are then compared against a single public input.
Note that this technique introduces a subtle problem: if the MAC key is known to the verifier, then the protocol is not zero-knowledge; however if the MAC key is known to the prover, then the MAC is not unforgeable (and the ZKP not sound). This tension is resolved by having the prover and verifier jointly sample the MAC key. I invite you to read more details in Section 3.4 of the paper.
Implementation techniques
Fast Reed-Solomon encoding in every field using convolutions
The Ligero proof system requires that the witness be encoded using a Reed-Solomon (RS) code. We usually perform this operation as follows: first, we interpret the witness vector as the evaluations of a polynomial over a set of roots of unity; we then interpolate the corresponding polynomial; finally, we evaluate it at a larger set of roots of unity. The above method requires the existence of roots of unity and uses an inverse FFT (and regular FFT) to perform polynomial interpolation (and evaluation, respectively). I’ll therefore refer to this method for RS encoding as the “pure-FFT method”.
To be compatible with all deployed standard curves for digital signatures, the libZK system needs to remain performant in contexts where roots of unity and FFTs are not available.
Naively interpolating and evaluating a polynomial is prohibitively slow for the prover.
Here, Frigo and Shelat use an observation from previous work by Cormode, Mitzenmacher and Thaler (2012): instead of interpolating and evaluating a polynomial, RS encoding can be done by computing a convolution.
Importantly, convolutions can be efficiently performed in any field using Nussbaumer’s algorithm, requiring $\mathcal{O}(n \log n \log\log n)$ field-operations.
When FFTs are available the convolution can be computed in $\mathcal{O}(n \log n)$ field-operations.
Whether or not FFTs are available and used, I refer to this method for RS encoding as the “convolution method”.
The convolution method offers two main benefits:
- this method is available even when roots of unity and FFTs are not. This is particularly important for systems like
libZKthat aim for maximum compatibility and may become a standard. - it allows us to pick arbitrary interpolation and evaluation domains for our polynomials. This is particularly helpful in contexts where we use a small field and a cryptographically-large extension. Indeed, we can define the interpolation and evaluation domains to be in the small field rather than in the extension as would be the case if we were using roots of unity (as per the pure-FFT encoding method). This results in RS codewords that are also defined in the small field (!), reducing proof size by a constant factor.
When FFTs are available, the convolution method (with FFTs) incurs a theoretical 2x overhead compared to the pure-FFT method. When I say “theoretical”, I am quoting Matteo and Abhi who have shared that the overhead can be eliminated in certain settings using known optimizations. However, and once again quoting private communications with the authors, “the whole point of the system is that the speed of the FFT does not matter much”. Indeed, they are only used to shave off a $\log \log n$ factor in encoding time; which is just one of many tasks run by the prover.
FFTs for secp256r1
Although not mission-critical, the existence of FFTs allows for faster prover runtimes. However, neither of the fields chosen above are FFT-friendly. Recall that an FFT-friendly field is one that has a multiplicative subgroup for which the size is a larger power of $2$. Equivalently, a field is FFT-friendly if its order $q$ is such that $q-1$ is divisible by a large power of $2$.
The base field of the secp256r1 elliptic curve is not FFT-friendly. Looking at the expression given for $p$ above, we can simplify it as $p := 2^{96} \cdot r - 1$. The size of the multiplicative subgroup of this field is $p-1 = 2^{96} \cdot r - 2 = 2 \cdot (2^{95} \cdot r-1)$. In other words, we have $2^1$ times some large odd number: definitely not FFT-friendly.
On the other hand, $\mathbb{F}_{p^2}$ the quadratic extension of $\mathbb{F}_p$ is FFT-friendly. Indeed, the order of $\mathbb{F}_{p^2}$ is $p^2$ and the order of the multiplicative subgroup is $p^2 - 1 = (p+1)(p-1) = 2^{96} \cdot r \cdot (p-1)$. And there is our large power of $2$, meaning that we can perform FFTs in the quadratic extension of $\mathbb{F}_p$. Concretely, this represents a 4x overhead compared to a similar-sized FFT-friendly field; but that is better than not doing FFTs or using an FFT-friendly field and implementing an ECDSA circuit with foreign-field arithmetic.
A connection to Virgo and Circle STARKs. In fact, we can apply the same idea to any prime $p’$: express it as $p’ := 2^\ell \cdot s - 1$ and then notice that $2^\ell$ divides $p’+1$, which itself divides ${(p’)}^2-1$, the order of the multiplicative subgroup of $\mathbb{F}_{(p’)^2}$. Setting $s=1$ gives us primes of the form $2^\ell - 1$; i.e., Mersenne primes as first used in Virgo and later in Circle STARK.
FFTs for binary fields
Performing FFTs for binary fields is just as miraculous and comes from a 2014 paper by Lin, Chung and Han, as exploited in Binius. Since this is a technique already known in our research and engineering community, I will conveniently avoid discussing it in this post (especially because I have not looked into how it works).
Circuit design: we stand on the shoulders of (digital hardware) giants
The final technique I wanted to highlight is how the authors of libZK borrowed techniques from digital hardware design to reduce the depth of their CBOR parsing circuit.
Writing an efficient circuit that parses a message and extracts features is hard:
write too many constraints and your prover will run forever;
write too few and you have a soundness bug.
The technique they use to keep their circuit short is known as “parallel-prefix”. It was originally designed to perform running sums in logarithmic time rather than linear time. Apparently the same method can be applying to parsing inputs. For more details I encourage you to read Section 4.3 of the paper and specifically the paragraph titled “Reducing the depth of lexing”.
Acknowledgements
Thank you to Alberto Centelles for improving this article through his many valuable suggestions. Thank you to Matteo Frigo and Abhi Shelat for reaching out, taking the time to clarify my confusion and explaining the relevant sections of the paper and existing works in great and invaluable detail.
Edit history
2 June, 2025: In the previous version of the post, I focused on how to compute FFTs in the secp256r1 base field and binary fields. That focus was somewhat misguided. The interesting insight is in how to efficiently compute Reed-Solomon encodings in any field using a convolution rather than the usual “interpolation and evaluation” method. In some fields, this convolution can be computed faster using FFTs. I explain all of this in further detail in the revised “implementation techniques” section. Changelog: the “implementation techniques” section and summary have been re-written, as well as the “connection to Circle STARK”; the acknowledgements now reflect the wonderful help and explanations I received from Matteo and Abhi. All other sections of the article remain unchanged.
-
Alternatively, in the case of interactive oracle proofs we run the BCS transform: we first commit to the prover’s oracle messages using Merkle trees and then apply the Fiat-Shamir transform. ↩︎