Functional Commitments: ZK under a different lens

This article is cross-posted from the Geometry Notebook and relates to an implementation co-written with Andrija Novakovic.

We thank Wilson Nguyen for insightful discussions about the protocol and Koh Wei Jie for his work on the implementation. Thank you to Tom Walton-Pocock and Koh Wei Jie (again) for their helpful comments towards this post.

In ZKP schemes, the typical paradigm is that a programme (or “circuit”) is publicly known, and a proof is produced to attest to the correct execution of the programme over some (potentially private) inputs. But what if we are working with sensitive, proprietary algorithms? Could we instead prove the execution of a private programme over public inputs?

Boneh, Nguyen and Ozdemir [BNO21]¹ offer to do just that by introducing function-hiding functional commitments. In this article, we review the main results presented in [BNO21], and give an overview of their SNARK-based construction.

A new primitive

Definition

Functional commitments can be understood as a generalisation of polynomial commitments to any function. The scheme allows a committer to produce a hiding and binding commitment to a function $f$ of their choice. Later a verifier may present an input $x$ to be evaluated. The committer can reply with a value $y$ and a (zero-knowledge) proof attesting to the fact that $f(x) = y$.

A more detailed description is given in the following extract from [BNO21]:

Applications

Functional commitments bring two important properties to applications. Firstly, like SNARKs, they allow service providers to convince users that everyone’s data is processed in the same way. Secondly, they prove that a ‘secret recipe’ was applied without the need to reveal it.

The reasons for hiding an algorithm while maintaining verifiability seem to fall under two generic categories:

1. To protect an evaluation function or test vector from cheaters. An example of this would be an online multiple-choice question exam for an official qualification. The examiner can commit to a secret marking scheme and later convince participants that they were all marked in the same way. Keeping the marking scheme private ensures that the answers do not leak. (Note that this does not guarantee that the marking scheme itself is fair!)
2. To protect a valuable algorithm. A service provider can commit to a proprietary machine learning model - say one that generates artworks from text prompts - for which users pay for each API call: the service provider can keep their model private while the client is convinced that the committed model was run.

Building functional commitments

One way to build a functional commitment is from a pre-processing zkSNARK. Recall that a pre-processing zkSNARK is a SNARK in which the circuit is encoded into an “index key” before any proof is generated. An initial construction would be to encode our function $f$ into a circuit and produce a pre-processing zkSNARK for it: the index key can be used as a commitment to the function and the proof can be used to implement the Evaluate protocol. This approach fails on two accounts, however [BNO21] fix both issues and obtain an efficient functional commitment scheme.

Index Privacy

The first hurdle is that the index key or the proving protocol might reveal information about the circuit. As it turns out, currently popular SNARK constructions such as Marlin and PLONK uphold the zero-knowledge property with respect to a witness but not the circuit. Consequently, Boneh, Nguyen and Ozdemir [BNO21] introduce the notion of an index-private proving system - one that perfectly hides the circuit - and show how to construct index-private variants of Marlin and PLONK.

Relations vs Functions

The second issue is more subtle: SNARKs, and proving systems in general, allow us to prove a statement about a relation. Relations are more general than functions: while a function allows only one output for each input (i.e. $f(x)$ is a unique value), relations allow for multiple assignments. Let’s illustrate this with two example circuits; we say that an instance-witness pair $(x,y)$ “satisfies” a circuit if the final wire evaluates to $0$.

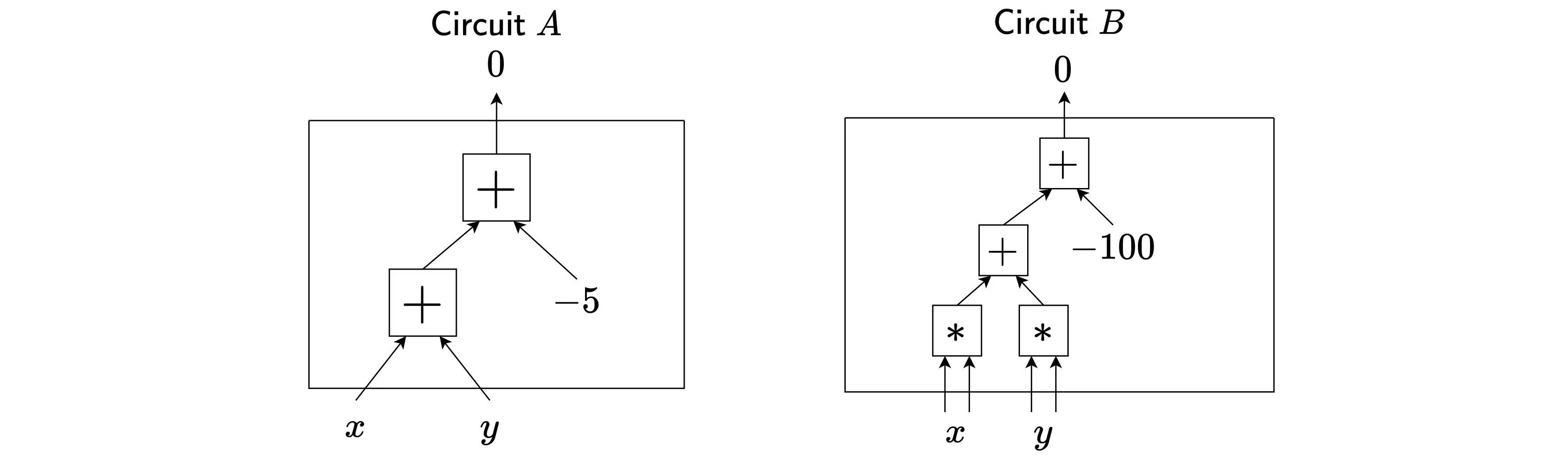
We can follow along the wires to write out the equations relating satisfactory instance-witness pairs: $$ \mathsf{Circuit} \; A: \quad x + y + (-5) = 0 \iff y = -x + 5 $$ $$ \mathsf{Circuit} \; B: \quad x^2 + y^2 + (-100) = 0 \iff x^2 + y^2 = 100 $$

Plotting these equations on the $x$-$y$ plane yields the following graphs (left: circuit $A$, right: circuit $B$):

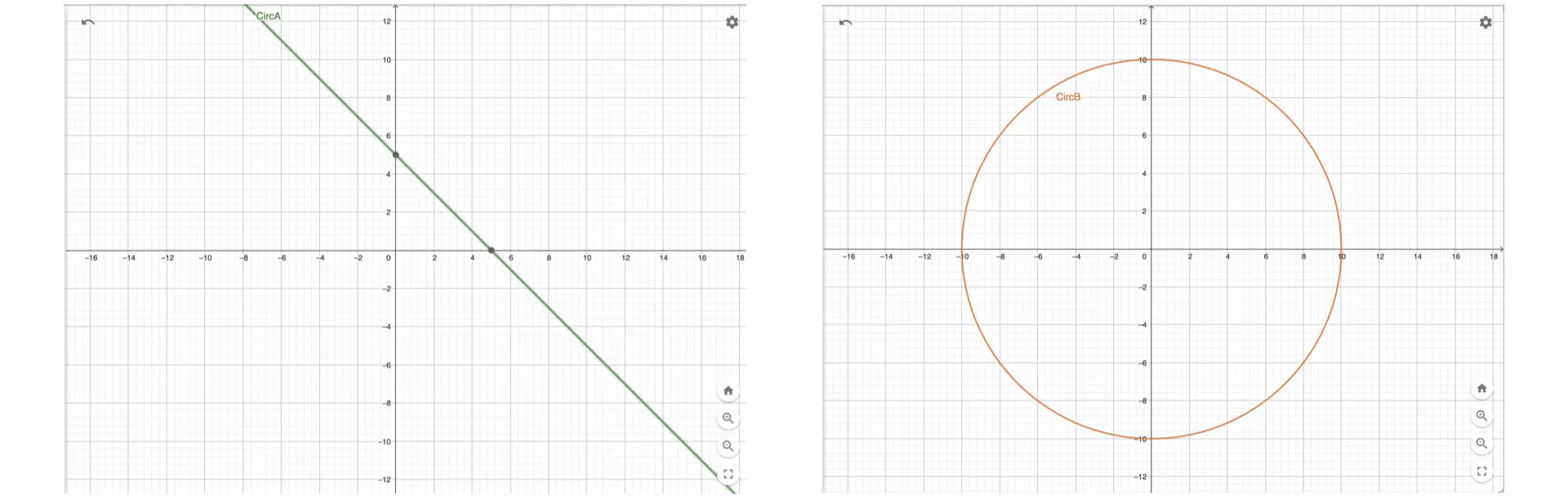
Notice that in circuit $A$, for a given $x$ value there is only one satisfying $y$ value. On the other hand, circuit $B$ allows for multiple satisfying $y$ values for a fixed $x$.

This property of relations would allow a prover to “cheat” the commitment scheme. For circuit $B$, given the value $x=0$ a malicious prover can now choose which value it wants to show ($y=10$ or $y=-10$). The circuit will be satisfied in both cases, however this ability to choose breaks the binding property of the functional commitment. What is worse, as the circuit is perfectly hidden the verifier has no means of checking whether it is in case $A$ or $B$!

Proof of Function Relation

[BNO21] fix this by introducing a zero-knowledge proof of function relation, efficiently proving that the circuit defines a function. The construction of such a proof depends on how the circuit is encoded by the proof system. Once again Boneh, Nguyen and Ozdemir [BNO21] show how to construct such proofs for R1CS (as used in Marlin) and the “vanilla” PLONK arithmetisation.

With index-private proving systems and proofs of function relation, we now have a construction for a functional commitment scheme: the commitment is the index key of an index-private pre-processing zkSNARK; evaluations can be checked by running the SNARK Verify algorithm and a proof of function relation for the index key.

Implementation

We provide a proof-of-concept implementation of the Marlin-based functional commitment scheme. The code is based on Arkworks and provides: 1) the compiler for circuit-to-“functional R1CS” described in Appendix D of [BNO21], 2) a modified version of Arkworks’ Marlin implementation to support index privacy and 3) a proof of function relation for R1CS-$f$.